| Hex Prefix | Base58 Leading Character | Represents | Example |
|---|---|---|---|
00 |
1 | Address (P2PKH) | 1AKDDsfTh8uY4X3ppy1m7jw1fVMBSMkzjP |
05 |
3 | Address (P2SH) | 34nSkinWC9rDDJiUY438qQN1JHmGqBHGW7 |
80 |
K, L, or 5 | WIF Private Key | L4mee2GrpBSckB9SgC9WhHxvtEgKUvgvTiyYcGu38mr9CGKBGp93 |
0488ADE4 |
xprv | Extended Private Key | xprv9tuogRdb5YTgcL3P8Waj7REqDuQx4sXcodQaWTtEVFEp6yRKh1CjrWfXChnhgHeLDuXxo2auDZegMiVMGGxwxcrb2PmiGyCngLxvLeGsZRq |
0488B21E |
xpub | Extended Public Key | xpub67uA5wAUuv1ypp7rEY7jUZBZmwFSULFUArLBJrHr3amnymkUEYWzQJz13zLacZv33sSuxKVmerpZeFExapBNt8HpAqtTtWqDQRAgyqSKUHu |
Base58
An easy-to-share set of characters
Base58 Character Set
0 1 2 3 4 5 6 7 8 9
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
a b c d e f g h i j k l m n o p q r s t u v w x y z
Base58 is a user-friendly set of characters you can use to represent big numbers in a shorter format.
Satoshi came up with this character set in the first release of Bitcoin. It is used for encoding legacy addresses, WIF private keys, and extended keys.
Terminology
What does "base58" mean?
The "base" refers to the number of characters you use to represent a value.
| Base | Characters |
|---|---|
| 2 (binary) | 01 |
| 10 (decimal) | 0123456789 |
| 16 (hexadecimal) | 0123456789abcdef |
| 58 | 123456789ABCDEFGH JKLMN PQRSTUVWXYZabcdefghijk mnopqrstuvwxyz |
In everyday life, we are used to working with base10 numbers (using the ten digits 0123456789).
But if you're a computer, it's easy enough to use extra characters to represent values:
base10(9999) = 9999
base16(9999) = 270f
base58(9999) = 3yQ
All of these "numbers" have the same value – they just use different character sets (i.e. bases) to represent them.
The more characters you have in your base, the fewer characters you need to use to represent big numbers.
Benefits
Why do we use Base58 in Bitcoin?
// Why base-58 instead of standard base-64 encoding? // - Don't want 0OIl characters that look the same in some fonts and // could be used to create visually identical looking account numbers. // - A string with non-alphanumeric characters is not as easily accepted as an account number. // - E-mail usually won't line-break if there's no punctuation to break at. // - Doubleclicking selects the whole number as one word if it's all alphanumeric.
Why Base58? Why these specific 58 characters?
Because these are the characters you are left with when you use all the characters in the alphanumeric alphabet (62 in total), but remove the easily mistakable characters 0, O, l, and I.
alphanumeric = 0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz
base58 = 123456789ABCDEFGH JKLMN PQRSTUVWXYZabcdefghijk mnopqrstuvwxyz
So base58 has two main benefits:
- It gives you a bigger set of characters to work with. This means you can represent larger numbers using fewer characters.
- It leaves out awkward characters. This helps to prevent mistakes when transcribing.
Encode
Convert an integer to Base58

To convert an integer (base10) to base58, you use the modulo1 function.
Basically, you keep dividing your number by 58, taking the remainder at each step of the way to get the index of the next base58 character, and you stop when there are no remainders left.
For example:
base10 = 123456789
123456789 % 58 = 19 <- remainder
2128565 % 58 = 23 <- remainder
36699 % 58 = 43 <- remainder
632 % 58 = 52 <- remainder
10 % 58 = 10 <- remainder
base58 = [10][52][43][23][19]
base58 = BukQL
Code

 copied
copied copied
copied# A simple function that converts an _integer_ to base58:
def int_to_base58(i)
characters = %w[
1 2 3 4 5 6 7 8 9
A B C D E F G H J K L M N P Q R S T U V W X Y Z
a b c d e f g h i j k m n o p q r s t u v w x y z
]
# create an empty string (in preparation to hold the new characters)
buffer = ''
# keep finding the remainder until our starting number hits zero
while i > 0
# find the remainder after dividing by 58 (% = modulo)
remainder = i % 58
# add the base58 character to the start of the string
buffer = characters[remainder] + buffer
# divide our integer by 58, and repeat...
i = i / 58
end
return buffer
end
puts int_to_base58(123456789) #=> BukQLDecode
Convert Base58 to an integer

To convert a base58 value into base10 (integer), working from right to left, you take the index for each Base58 character and multiply it by increasing powers of 58, then add all the values together.
For example:
base58 = BukQL
L = 19 * 58^0 = 19
Q = 23 * 58^1 = 1334
k = 43 * 58^2 = 144652
u = 52 * 58^3 = 10145824
B = 10 * 58^4 = 113164960
base10 = 19 + 1334 + 144652 + 10145824 + 113164960
base10 = 123456789
Code

 copied
copied copied
copieddef base58_to_int(base58)
characters = %w[
1 2 3 4 5 6 7 8 9
A B C D E F G H J K L M N P Q R S T U V W X Y Z
a b c d e f g h i j k m n o p q r s t u v w x y z
]
# create an integer to hold the result
total = 0
# reverse the base58 string so we can read characters from right to left
base58 = base58.reverse
# run through each character, including the index, so we know how many characters we've read
base58.each_char.with_index do |char, i|
# get the index number for this character
char_i = characters.index(char)
# work out how many 58s this character represents (increment the power for each character)
value = char_i * (58**i)
# add to total
total = total + value
end
return total
end
puts base58_to_int("BukQL") #=> 123456789This mathematical process is the same when converting from one base to another. You can see a similar example when converting from hexadecimal to decimal (base16 to base10).
Base58 in Bitcoin
How is Base58 used in Bitcoin?
Base58 is used in Bitcoin when you want to convert commonly used data into an easier-to-share format. For example:
- Addresses
- A public key is the "public" counterpart to a private key, and you use them when you want to send bitcoins to someone. However, public keys are quite lengthy, so we convert them to addresses instead (which makes use of base58 in the final step of the conversion).
- WIF Private Keys
- A private key is like a "password" that you use to unlock bitcoins for spending, and sometimes you may want to import one into a wallet. For this occasion there is such a thing as a WIF Private Key, which is basically a private key converted to base58.
- Extended Keys
- If you're using an HD Wallet, you may come into contact with extended private keys and extended public keys. These are also converted to base58 to shorten them and make them easier to share.
Base58 was only used for encoding addresses at first, but was utilized for encoding WIF Private Keys and extended keys when they were introduced later on.
Leading Zeros

In Bitcoin, we convert every zero byte (0x00) at the start of a hexadecimal value to a 1 in base58.
Putting zeros at the start of a number does not increase its size (e.g. 0x12 is the same as 0x0012), so when we convert to base58, any additional zeros at the start do not affect the result.
Therefore, to ensure that leading zeros have an influence on the result, the bitcoin base58 encoding includes a manual step to convert all leading 0x00's to 1's.
0x: A 0x prefix indicates a hexadecimal value. Hexadecimal values will sometimes only contain the numbers 0-9 and could therefore be confused as being decimal values, so the prefix helps us to distinguish between them. This prefix is discarded before being used in calculation.
Byte: A byte of data can hold a value of between 0-255, and can be represented by two hexadecimal characters. For example, 0xff is one byte of data and represents the value 255 in decimal.
Prefixes
In Bitcoin, different prefixes are added to data before converting to base58 to influence the leading character of the result, and this leading character helps us to identify what each base58 string represents.
These are the most common prefixes used in Bitcoin:
| Hex Prefix | Base58 Leading Character | Represents | Example |
|---|---|---|---|
6F |
m or n | Address (P2PKH) | ms2qxPw1Q2nTkm4eMHqe6mM7JAFqAwDhpB |
C4 |
2 | Address (P2SH) | 2MwSNRexxm3uhAKF696xq3ztdiqgMj36rJo |
EF |
c or 9 | WIF Private Key | cV8e6wGiFF8succi4bxe4cTzWTyj9NncXm81ihMYdtW9T1QXV5gS |
04358394 |
tprv | Extended Private Key | tprv9tuogRdb5YTgcL3P8Waj7REqDuQx4sXcodQaWTtEVFEp6yRKh1CjrWfXChnhgHeLDuXxo2auDZegMiVMGGxwxcrb2PmiGyCngLxvLeGsZRq |
043587CF |
tpub | Extended Public Key | tpub67uA5wAUuv1ypp7rEY7jUZBZmwFSULFUArLBJrHr3amnymkUEYWzQJz13zLacZv33sSuxKVmerpZeFExapBNt8HpAqtTtWqDQRAgyqSKUHu |
https://en.bitcoin.it/wiki/List_of_address_prefixes
WIF Private Keys use the same hex prefix, but produce different leading characters. This is because in some situations we append an 01 byte to the private key before converting to base58, and this extra byte affects the leading character.
Extended Keys contain extra metadata alongside the original public and private keys, which is why their base58 strings are noticeably longer.
Base58Check
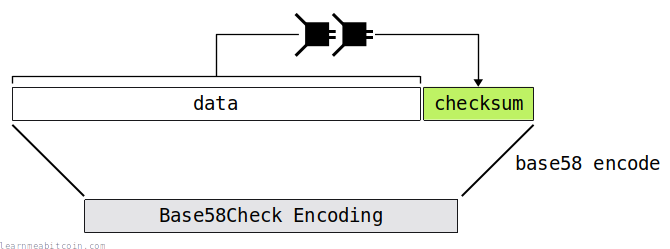
Base58Check encoding is short for adding a checksum to some data before encoding it to base58.
Here are some common examples of Bitcoin data that use Base58Check encoding:
You sometimes see this "Base58Check" term pop up every now and then when reading about base58 encoding, so I thought I'd cover it here.
Code
These code snippets perform the complete base58 conversion used in Bitcoin.
They convert to and from hexadecimal, because that's the most common format we start with when converting to base58.

 copied
copied copied
copiedmodule Base58
@chars = %w[
1 2 3 4 5 6 7 8 9
A B C D E F G H J K L M N P Q R S T U V W X Y Z
a b c d e f g h i j k m n o p q r s t u v w x y z
]
@base = @chars.length
def self.encode(hex)
i = hex.to_i(16)
buffer = String.new
while i > 0
remainder = i % @base
i = i / @base
buffer = @chars[remainder] + buffer
end
# add '1's to the start based on number of leading bytes of zeros
leading_zero_bytes = (hex.match(/^([0]+)/) ? $1 : '').size / 2
("1"*leading_zero_bytes) + buffer
end
def self.decode(base58)
total = 0 # integer to hold conversion to decimal
# run through each character
base58.reverse.each_char.with_index do |char, i|
char_i = @chars.index(char) # get the index number for this character
value = (58**i) * char_i # work out how many 58s this character represents
total = total + value # add to total
end
# convert this integer to hex
hex = total.to_s(16)
# add leading 00s for every leading 1
leading_1s = (base58.match(/^([1]+)/) ? $1 : '').size
("00"*leading_1s) + hex
end
end
puts Base58.encode('0093ce48570b55c42c2af816aeaba06cfee1224faebb6127fe') #=> 1EUXSxuUVy2PC5enGXR1a3yxbEjNWMHuem
puts Base58.decode('1EUXSxuUVy2PC5enGXR1a3yxbEjNWMHuem') #=> 0093ce48570b55c42c2af816aeaba06cfee1224faebb6127fe

 copied
copied copied
copied<?php
// Sample Input
$hex = "00662ad25db00e7bb38bc04831ae48b4b446d1269817d515b6"; // a public key hash (with a 00 prefix)
// -------------
// Base58 Encode
// -------------
// Convert hex string to an integer
$num = gmp_init($hex, 16);
$base58 = "";
// Base58 Characters
$chars = str_split("123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz");
// Keep dividing by 58 and taking the remainder as the character
while ($num > 0) {
$rem = gmp_mod($num, 58); // remainder (what we get the character for)
$num = gmp_div($num, 58); // quotient (keep dividing the number to get remainders)
$base58 = $chars[intval($rem)].$base58; // add base58 char to the start
}
// Convert leading 00s in hex to leading 1s (this is done manually in the base58 conversion)
$count = intval(strspn($hex, "0") / 2); // how many leading 0s, then divide by 2 (to work out how many zero bytes have been prefixed)
$leading = str_repeat("1", $count); // prefix one leading 1 for every zero byte (e.g. 00)
// Result
$result = $leading.$base58;
echo $result.PHP_EOL; // 1AKDDsfTh8uY4X3ppy1m7jw1fVMBSMkzjP
// -------------
// Base58 Decode
// -------------
$base58 = "1AKDDsfTh8uY4X3ppy1m7jw1fVMBSMkzjP";
$int = gmp_init(0); // integer to hold result
// Convert to decimal
$base58a = str_split(strrev($base58)); // create an array we can loop through
foreach ($base58a as $i => $c) { // run through each character
$multiple = gmp_pow(58, $i); // how many 58s this position holds (e.g. 58^0, 58^1, 58^2...)
$index = array_search($c, $chars); // get index number for base58 char (e.g. B=10)
$value = gmp_mul($index, $multiple); // multiply to get number of 58s this character is representing
$int = $int + $value; // add to total
}
// Convert to hexadecimal
$gmp = gmp_init(strval($int), 10); // create gmp number from bit string (base 10) NOTE: gmp_init takes strings
$hex = gmp_strval($gmp, 16); // convert to hex string representation
if (strlen($hex) % 2 !== 0) { // return even number of characters (hex2bin prefers it)
$hex = '0'.$hex;
}
// Convert leading 1s in base58 to leading 00s (this is done manually in the base58 conversion)
$count = strspn($base58, "1");
$leading = str_repeat("00", $count);
// Result
$result = $leading.$hex;
echo $result.PHP_EOL; // 00662ad25db00e7bb38bc04831ae48b4b446d1269817d515b6
Notes
Modulo (%)
The modulo (%) operator returns the remainder of a division:
7 % 6 = 1
7 % 5 = 2
7 % 4 = 3
7 % 3 = 1
It's like a sister of the divide (/) operator.
Resources
- src/base58.cpp
- github.com - base58.rb
- bitcoin.it/wiki/Base58Check_encoding
- darklaunch.com - Base58 Encoder/Decoder
Further Reading
Thanks
- TheSeven - Chatted on IRC. Helped me to understand how Base58 is implemented in Bitcoin.