Private Keys
What is a private key?
A private key is a large randomly-generated number.
For example:
But to be more precise, a private key is a random 256-bit number:
Yes, this is still a number. It's just in binary, which is how numbers are stored in a computer. Because you know, Bitcoin is a computer program after all.
Anyway, we can easily convert this private key from binary to decimal:
Or to hexadecimal:
It doesn't make a difference. They're all the same number, and they're all the same private key.
Because after all, a private key is just a number.
A raw private key is typically displayed in hexadecimal format.
What is a 256-bit number?
A 256-bit number is a number that can be stored inside 256 bits of data.
What is a bit?
A bit is the smallest unit of data inside a computer.
| Unit | Size |
|---|---|
| gigabyte | 1000 megabytes |
| megabyte | 1000 kilobytes |
| kilobyte | 1000 bytes |
| byte | 8 bits |
| bit |
In fact, a bit is so small, it can only hold a value of 1 or 0:

Nonetheless, you can still use bits to represent other kinds of data, such as everyday numbers.
For example, here's how you would store the decimal numbers 0 to 8 in a computer using bits:
Therefore, a 256-bit number is a number that can be represented by using 256 of these bits:

Or in other words, a 256-bit number is between:
min: 0
max: 115792089237316195423570985008687907853269984665640564039457584007913129639935
So as you can see, 256 bits gives you room to use some pretty big numbers.
And that's all 256-bit numbers are; numbers that fit inside 256 bits of data.
The maximum number of 256-bit numbers is equal to 2256.
Where do private keys come from?
I wasn't lying when I said they are generated randomly.
Honestly, when you use any kind of bitcoin software to generate a private key, they are not performing magic – they're just giving you a random 256-bit number.
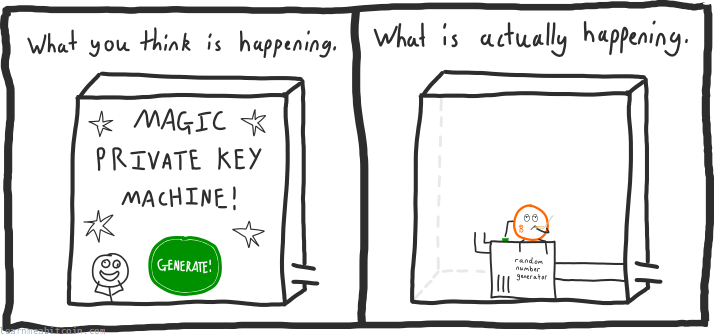
Therefore, there's no reason why you can't create your own private key. All you need is to be able to securely generate a random 256-bit number.
You can do this in a number (heh) of ways:
1. Flip a coin 256 times.
Flipping a coin 256 times allows you to generate a 256-bit private key in binary:
This 256-bit binary result can then be converted to hexadecimal.
2. Use your favorite programming language.
This will give you a private key in decimal:

 copied
copied copied
copied# need to use the operating system's random number generator for security
import random
random.SystemRandom().randint(1, 115792089237316195423570985008687907852837564279074904382605163141518161494336)Be careful when generating random numbers using a programming language. The default "random" functions in most programming languages aren't usually random enough, so make sure that the function you're using is described as being "cryptographically secure".
3. Hash some random data using the SHA-256 hash function.
Inserting random data into the SHA-256 will return a 32-byte (256-bit) hexadecimal result, which can be used as a private key:

The data you hash must be suitably large and random. Putting the word "bitcoin" into the SHA256 hash function (and using that as your private key) is not going to be secure.
All of these methods will give you a 256-bit number. And if you've got a 256-bit number, you've got a private key.
Your private keys must be random.
If you use a random number generator that isn't reliably random (i.e. it has patterns in the way it generates random numbers), you're leaving yourself vulnerable to anyone who is familiar with the weaknesses of the random number generator you used.
And if someone is able to recreate the same private key as you, they can take your bitcoins.
As a result, most guides will make you fearful about generating your own private keys, because nobody wants to be responsible for your mistakes.
But don't let all that fearmongering stop you. As long as you're cautious you'll be fine.
A valid private key is actually slightly less than the maximum 256-bit number. So if you're generating a private key, you will need to check that it's within the valid range before trying to use it. It's rare that this happens, but it's important to check.
The fact that anyone can create their own "account" by simply generating a random number is an important feature of Bitcoin. It means that no one is in control of issuing accounts, which means bitcoin is accessible to anyone who can generate a large random number.
What if someone generates the same private key as me?
Then they'll be able to steal your bitcoins.
But don't worry, nobody is going to randomly generate the same private key as you.
Surely they could?
Okay, they theoretically could, but due to the range of possible private keys, it's somewhat "unlikely".
For example, if I had one million monkeys who could each generate one million private keys per second (I've trained them well), it would take 3,671,743,063,080,803,235,470,924,132,853,876,261,056,103,149,731,840 million years (roughly) for them to generate every single possible private key.
Now, if you're attempting a brute-force search to find someone else's private key, on average you'll need to run through half of all the possible private keys before finding the one you're looking for, which means these monkeys are looking at 1,835,871,531,540,401,617,735,462,066,426,938,130,528,051,574,865,920 million years of work if they want to generate the exact same private key as you.

 copied
copied copied
copiedkeys = 115792089237316195423570985008687907852837564279074904382605163141518161494336
monkeys = 1000000
rate = 1000000
keyspersecond = monkeys * rate
seconds = keys / keyspersecond
minutes = seconds / 60
hours = minutes / 60
days = hours / 24
years = days / 365
millionyears = years / 1000000
print(round(millionyears)) #=> 3671743063080803235470924132853876261056103149731840 (all private keys)
print(round(millionyears / 2)) #=> 1835871531540401617735462066426938130528051574865920 (average time to find someone else's key)So as you can see, I haven't quite got the time or monkey-power on my side. And neither has anyone else.
There are so many possible private keys that choosing one at random is secure enough in itself.
Fair enough.
I'm not done yet.
The range of 256-bit numbers (and therefore the number of possible private keys) is unfathomably large. Just as it's impossible for the human mind to visualize the true scale of the universe, it's impossible for the human mind to comprehend the sheer size of 256-bit numbers.
So if you have any doubts about the safety of your 256-bit number, it's either because you didn't use a reliable enough random number generator, or because you don't appreciate the magnitude of the numbers we are dealing with.
Now get out of my office.