Public Keys

A public key is the counterpart to a private key.

And similar to a private key, it's displayed as a hexadecimal string.

For example:

02c2c1d7120003416e229e041d4fec2e79343630a76bec7470308d9d4e6e5437a7

If we didn't end up shortening this public key to an address, this would be the "account number" that you send bitcoins to when making a transaction.

Anyway, here's the interesting part: your public key is calculated from your private key.

How do you get a public key from a private key?

You insert a private key into a special mathematical function, and the result is a public key.

What is this function?

It's called elliptic curve multiplication.

This basically involves "bouncing" around the graph of an elliptic curve until you end up at a final set of co-ordinates on the graph, and these resulting co-ordinates are your public key.

It'll be easier if I show you...

What does an elliptic curve look like?

Like this:

Furthermore, the elliptic curve used in Bitcoin comes with a specific starting point.

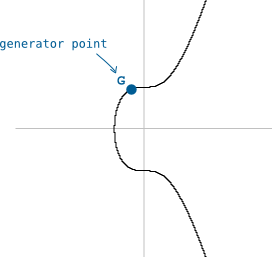
We call this starting point the generator point (G).

And if we were to do some "multiplication" on this curve (e.g. "multiplying" the starting point by 2), we would move around the curve like this.

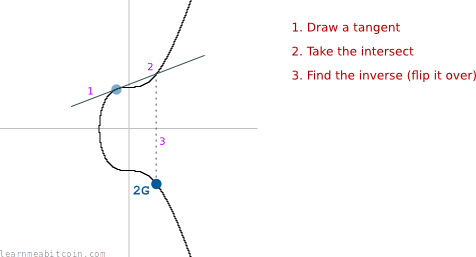
The fact that we can draw a tangent anywhere on the curve and it intersects one other point on the curve is a special feature of elliptic curves.

And there we have it. We have just "multiplied" the starting co-ordinate G by 2, and found the position of the final co-ordinate 2G.

This is one round of elliptic curve multiplication.

How do you create a public key?

In the above example we multiplied G by 2 to get 2G.

To get a public key, we multiply G by our private key.

private key = 1458d68874baf3e56083de30e338e2033246a392ab9c91638ea6a7647211c9f2
private key = 9203220165929919222843002161964433210421678620720351651223789246477071665650

public key  = 9203220165929919222843002161964433210421678620720351651223789246477071665650 * G

Or in other words, "bounce around the elliptic curve private key number of times".

The final resting point on the elliptic curve will give you a set of co-ordinates, and these co-ordinates form the public key.

So if these are the coordinates we end up with after multiplying G by our private key:

x = 88091178469400846770681149409605355642830909864371625742864066149995104188327
y = 45152788091227050158861436381847632561803984519000285563044048080157446820782

Then all we have to do is convert both to hexadecimal and smush them together...

public key (x) = c2c1d7120003416e229e041d4fec2e79343630a76bec7470308d9d4e6e5437a7
public key (y) = 63d39289162ec72eef96db15718861c34214fd668afc163b4e2f88435d6cd3ae

public key (x,y) = c2c1d7120003416e229e041d4fec2e79343630a76bec7470308d9d4e6e5437a763d39289162ec72eef96db15718861c34214fd668afc163b4e2f88435d6cd3ae

And ta da! A public key!

public key = 04c2c1d7120003416e229e041d4fec2e79343630a76bec7470308d9d4e6e5437a763d39289162ec72eef96db15718861c34214fd668afc163b4e2f88435d6cd3ae

Compressed Public Keys

To save space, public keys (these days) use the full x coordinate only.

This is because the elliptic curve is an equation (y^2 = x^3 + 7), which means that if you have the x co-ordinate, you can work out the corresponding y co-ordinate.

However, due to the y^2 part of the equation, the y could be a positive or negative number:

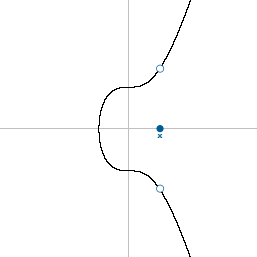
So the only extra information you need to find the correct y co-ordinate is to know whether the y co-ordinate is above or below the x-axis. And due to the way elliptic curves work:

• If y is even, it's above the x-axis.
• If y is odd, it's below the x-axis.

So instead of having to store both the full x and y co-ordinates, you can just store the full x co-ordinate, and whether the y co-ordinate is even or odd.

In Bitcoin, the polarity of the y co-ordinate is represented by a prefix:

• 02 = even
• 03 = odd

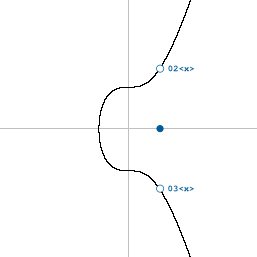
So whereas an old-school uncompressed public key will begin with 04, a compressed public key will begin with either 02 or 03:

public key (uncompressed) = 04c2c1d7120003416e229e041d4fec2e79343630a76bec7470308d9d4e6e5437a763d39289162ec72eef96db15718861c34214fd668afc163b4e2f88435d6cd3ae
public key (compressed)   = 02c2c1d7120003416e229e041d4fec2e79343630a76bec7470308d9d4e6e5437a7

Much shorter.

This seems like a lot of effort to save on a small amount of data, but because public keys are used within almost all transactions, it does end up saving a lot of space in the blockchain over time.

Why do we use elliptic curve multiplication to make public keys?

Because elliptic curves have two useful properties when creating a private/public key pair.

1. Elliptic curve multiplication is a "trapdoor function". In other words, you can't go backwards from public key to find out what the private key was.
   

   A trapdoor function is a function that is easy to compute in one direction, yet difficult to compute in the opposite direction (finding its inverse) without special information, called the "trapdoor".

2. The public key has a mathematical connection to the private key. As a result, it's possible to prove this connection (with a little more mathematics) without having to reveal your private key.

   So if I give you my public key (or address), I can prove to you that I "own" it without having to show you my private key.

   This feature is especially handy when making bitcoin transactions. Your public key can be placed into a transaction when you want to receive bitcoins, and you do not have to reveal the private key directly when you want to spend them later on (see digital signatures). As a result, this means that nobody can acquire the private key and use it to spend bitcoins that have been locked to the same public key.

   When I say prove that I own a public key, I mean "show that I possess the private key that the public key was created from".

How can you prove you own a public key?

This is a whole topic (or two) in itself. But seeing as this is such an annoyingly relevant question, I'll try my best to cover the basics.

As mentioned, there's a mathematical connection between the private key and public key.

As a result:

1. I can put my private key through some more elliptic curve mathematics to get a new value (called a digital signature).
2. I can put my public key through some other elliptic curve mathematics to get a new value.

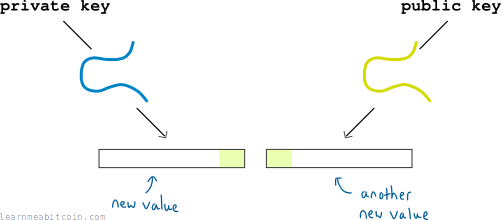
Now, there will be some small overlap between these new values:

And this overlap is enough to prove that there is a mathematical connection between the public key and private key.

And because nobody is able to recreate this digital signature without the private key, my digital signature it's enough to prove that I "own" the public key.

As a result, I can show you that I own a public key with a digital signature, and you never need to see my private key.

Conclusion

All hail the elliptic curve.