Merkle Root

Fingerprint for the transactions in a block

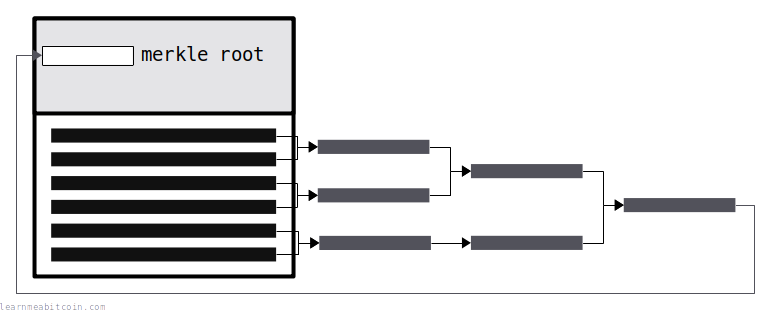
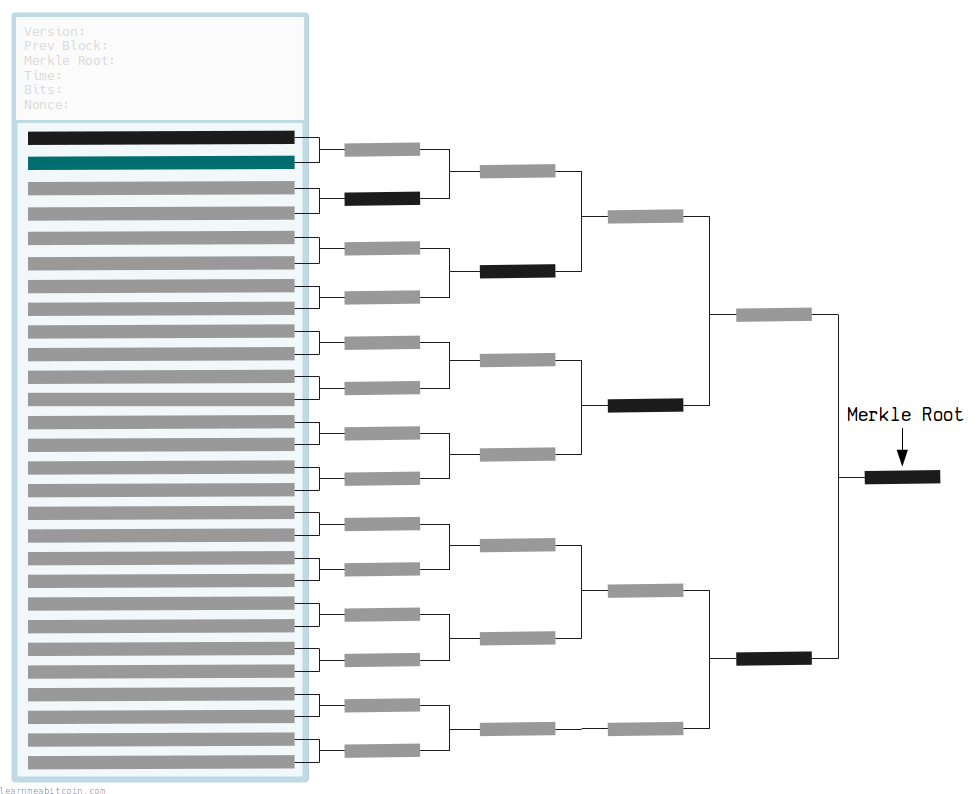
A merkle root is created by hashing together pairs of TXIDs to get a short and unique fingerprint for all the transactions in a block.

This merkle root is placed in a block header to prevent the contents of the block from being tampered with later on. So if someone tries to add or remove a transaction from the block, the merkle root for the transactions inside the block will no longer match the merkle root inside the block header.

In other words, the merkle root is what connects the block header to the transactions in the block.

Structure

How do you create a merkle root?

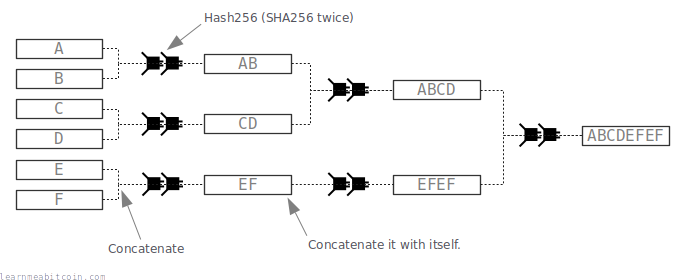
A merkle root is created by hashing TXIDs in a tree-like structure.

Hash the TXIDs together in pairs.
- Note: If you have a single item left over, hash it with itself.
Take the resulting hashes and hash those together in pairs.
Repeat until you are left with a single hash.

Technical diagram of a merkle tree structure.

Code

Here's some Ruby code for creating a merkle root from a list of TXIDs. The code is fairly readable, so it's worth reading through the steps even if you don't consider yourself to be a programmer.

require 'digest' # Need this for the SHA256 hash function

# Hash function used in the merkle root function (and in bitcoin in general)
def hash256(hex)
    binary = [hex].pack("H*")
    hash1 = Digest::SHA256.digest(binary)
    hash2 = Digest::SHA256.digest(hash1)
    result = hash2.unpack("H*")[0]
    return result
end

def merkleroot(txids)

  # Exit Condition: Stop recursion when we have one hash result left
  if txids.length == 1
    # Convert the result to a string and return it
    return txids.join('')
  end
  
  # Keep an array of results
  result = []

  # 1. Split up array of hashes in to pairs
  txids.each_slice(2) do |one, two|
    # 2a. Concatenate each pair
    if (two)
      concat = one + two
    # 2b. Concatenate with itself if there is no pair
    else
      concat = one + one
    end

    # 3. Hash the concatenated pair and add to results array
    result << hash256(concat)
  end

  # Recursion: Do the same thing again for these results
  merkleroot(result)
end


# Test (e.g. block 000000000003ba27aa200b1cecaad478d2b00432346c3f1f3986da1afd33e506)
txids = [
  "8c14f0db3df150123e6f3dbbf30f8b955a8249b62ac1d1ff16284aefa3d06d87",
  "fff2525b8931402dd09222c50775608f75787bd2b87e56995a7bdd30f79702c4",
  "6359f0868171b1d194cbee1af2f16ea598ae8fad666d9b012c8ed2b79a236ec4",
  "e9a66845e05d5abc0ad04ec80f774a7e585c6e8db975962d069a522137b80c1d"
]

# TXIDs must be in natural byte order when creating the merkle root
txids = txids.map {|x| x.scan(/../).reverse.join('') }

# Create the merkle root
result = merkleroot(txids)

# Display the result in reverse byte order
puts result.scan(/../).reverse.join('') #=> f3e94742aca4b5ef85488dc37c06c3282295ffec960994b2c0d5ac2a25a95766

Byte Order: The TXIDs must be in natural byte order when creating the merkle root. The resulting merkle root will also be in natural byte order, but it gets displayed in reverse byte order on blockchain explorers.

If there is only one transaction in a block, the merkle root will be the same as the TXID for that transaction.

Merkle Tree

Why do we use a merkle root?

This structure for hashing a list of items together is known as a merkle tree. But why use a merkle tree?

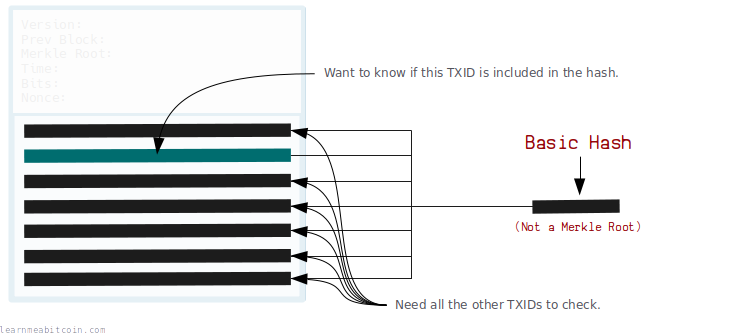
I mean we could just hash all the TXIDs together in one go. That would create a fingerprint for all the transactions in the block, and that would work. But later on if we wanted to find out if a specific TXID was used to create that fingerprint, we would need to know all the other TXIDs:

Without a merkle tree you would need all of the TXIDs in the block to recreate the final hash.

This is where merkle trees come in. If we use a merkle tree instead, we only need to know some of the branches along the path of the tree to check that a TXID was used to create the root hash:

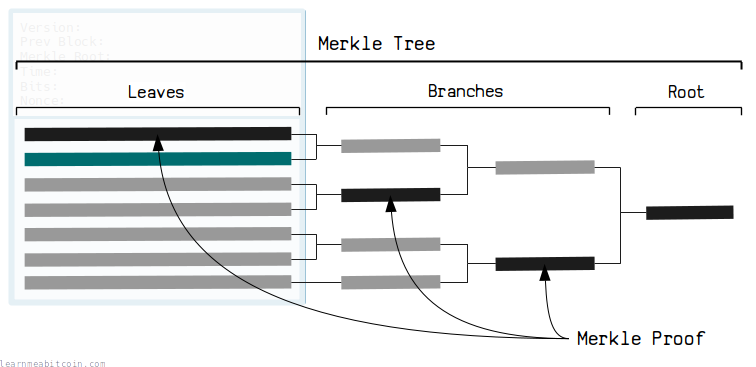
With a merkle tree you only need the specific branches (the merkle proof) to reconstruct the final hash (the merkle root)

This pathway is known as the merkle proof.

So by using a merkle tree, we can find out if a transaction is part of a block without having to know every other TXID in the block. Or in technical terms, a merkle tree provides an efficient way to prove that something is in a set, without having to know the full set.

And if you're dealing with blocks that have 2,000+ transactions in them, merkle trees become much more efficient than having all the TXIDs hashed together in one go.

Diagram showing how merkle trees save on bandwidth when verifying the presence of a transaction in larger blocks.

Merkle Proof Example

Let's say we have a block header (and therefore the merkle root) for the block 00000000000000000027ad67588ebcf18eabe2250c411e6b79ad1c009b4cb54f.

Now let's say we want to check that the transaction f66f6ab609d242edf266782139ddd6214777c4e5080f017d15cb9aa431dda351 is inside this block.

Here's the merkle proof that proves the transaction is inside the block:

txid
----
f66f6ab609d242edf266782139ddd6214777c4e5080f017d15cb9aa431dda351 (reverse byte order)

merkle proof
------------
50ba87bdd484f07c8c55f76a22982f987c0465fdc345381b4634a70dc0ea0b38 left
96b8787b1e3abed802cff132c891c2e511edd200b08baa9eb7d8942d7c5423c6 right
65e5a4862b807c83b588e0f4122d4ca2d46691d17a1ec1ebce4485dccc3380d4 left
1ee9441ddde02f8ffb910613cd509adbc21282c6e34728599f3ae75e972fb815 left
ec950fc02f71fc06ed71afa4d2c49fcba04777f353a001b0bba9924c63cfe712 left
5d874040a77de7182f7a68bf47c02898f519cb3b58092b79fa2cff614a0f4d50 left
0a1c958af3e30ad07f659f44f708f8648452d1427463637b9039e5b721699615 left
d94d24d2dcaac111f5f638983122b0e55a91aeb999e0e4d58e0952fa346a1711 left
c4709bc9f860e5dff01b5fc7b53fb9deecc622214aba710d495bccc7f860af4a left
d4ed5f5e4334c0a4ccce6f706f3c9139ac0f6d2af3343ad3fae5a02fee8df542 left
b5aed07505677c8b1c6703742f4558e993d7984dc03d2121d3712d81ee067351 left
f9a14bf211c857f61ff9a1de95fc902faebff67c5d4898da8f48c9d306f1f80f left

merkle root
-----------
17663ab10c2e13d92dccb4514b05b18815f5f38af1f21e06931c71d62b36d8af (reverse byte order)

This merkle proof contains a list of the branches across the merkle tree that we need to get to the merkle root. These branches also indicate whether they are on the "left" or "right" so that you can concatenate each pair in the correct order when hashing them together.

To check if the TXID forms part of the merkle root, we just start with the TXID, then recursively concatenate and hash through this merkle proof to confirm that we get the same result as the merkle root as found in the block header.

Lightweight Wallets

Thanks to merkle trees, you can create lightweight wallets (or "thin nodes") that can verify when a transaction has made it in to a block, without the overhead of having to download and store the entire the blockchain.

These wallets just download and store block headers (80 bytes each, instead of 1 MB+ blocks), and use the merkle roots inside them (along with merkle proofs they receive from full archival nodes) to verify that a transaction has made it in to a block.

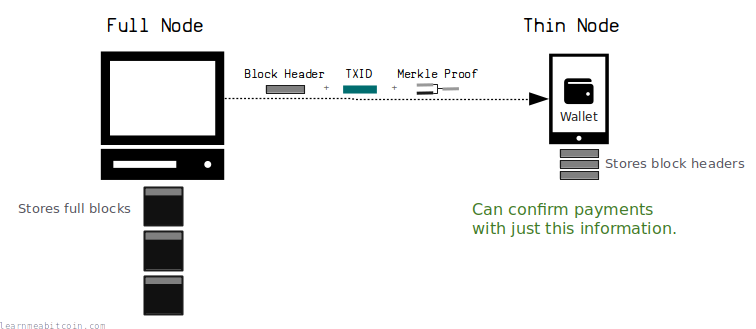
Block headers are just 80 bytes, whereas each block can be 1,000,000+ bytes.

A popular example of a lightweight wallet is Electrum.

I have no experience with these though, so here are some interesting links instead:

Why is it called a "merkle root"?

Because Ralph Merkle patented the idea in 1979.

Common Misconception.

Resources

Thanks

Thanks to Gabriele Semeraro for pointing out an error in the Ruby code. I had the exit condition for returning the result after the part where the pairs of TXIDs get hashed. But if you've only got one item left, you just return it without doing any more work. In other words, if you've only got one transaction in a block, the merkle root is the same as the TXID.