Public Key

A point on the elliptic curve

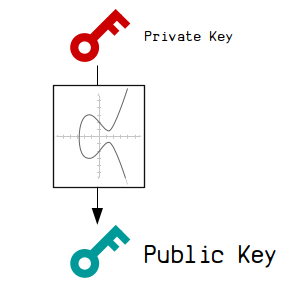
A public key is the "public" part of a private key and public key pair.

It's calculated from the private key, which means there is a mathematical connection between the two.

tool-680af545078ca

Public Key

Calculate the public key from a private key.

Private Key 0 bytes Public Key

Coordinates

parity:

A public key is just a point on an elliptic curve. The final public key is these coordinates in hexadecimal.

Compression Compressed (02 or 03 prefix) Uncompressed (04 prefix) x-only (no prefix)

The elliptic curve is symmetrical along the x-axis, so a compressed public key only needs to store the full x-coordinate and whether the y-coordinate is even or odd.

An x-only public key is used in Taproot outputs. The corresponding y-coordinate is assumed to be even.

0 bytes

Never enter your private key into a website, or use a private key generated by a website. Websites can easily save the private key and use it to steal your bitcoins.

0 secs

The public key is used so that you can "receive" bitcoins. When you make a transaction, an output can be locked to a public key, so that only the owner of the private key is able to unlock it and spend it in a future transaction.

Creating

How do you create a public key?

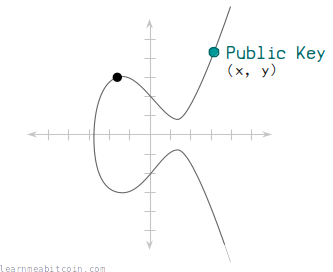
Diagram showing a public key as a point on an elliptic curve.

A public key is created via elliptic curve multiplication.

In technical terms, you multiply a starting point (generator point) on the secp256k1 elliptic curve by the private key (a random number), and this results in a new set of x and y coordinates, which is the public key.

Private Key

EC Multiply

So a public key is just a point on the elliptic curve.

I won't bore you with the details of elliptic curve mathematics at this stage, as you don't need to understand it to be able to create your own public keys. But you can look into it if you want to, and the mathematics isn't as difficult as it sounds.

Code

# example private key
private_key = "ef235aacf90d9f4aadd8c92e4b2562e1d9eb97f0df9ba3b508258739cb013db2"

# --------------------------
# Secp256k1 Curve Parameters
# --------------------------
# y^2 = x^3 + ax + b
$a = 0
$b = 7 # using global variables for convenience

# prime modulus
$p = 2 ** 256 - 2 ** 32 - 2 ** 9 - 2 ** 8 - 2 ** 7 - 2 ** 6 - 2 ** 4 - 1

# number of points on the curve
$n = 115792089237316195423570985008687907852837564279074904382605163141518161494337

# generator point (the starting point on the curve used for all calculations)
$g = {
  x: 55066263022277343669578718895168534326250603453777594175500187360389116729240,
  y: 32670510020758816978083085130507043184471273380659243275938904335757337482424,
}

# --------------------------
# Elliptic Curve Mathematics
# --------------------------
# Modular Inverse - Ruby doesn't have a built-in function for finding modular inverses, so here's one using the extended Euclidean algorithm.
def modinv(a, m = $p)
  m_orig = m         # store original modulus
  a = a % m if a < 0 # make sure a is positive
  y_prev = 0
  y = 1
  while a > 1
    q = m / a

    y_before = y # store current value of y
    y = y_prev - q * y # calculate new value of y
    y_prev = y_before # set previous y value to the old y value

    a_before = a # store current value of a
    a = m % a # calculate new value of a
    m = a_before # set m to the old a value
  end
  return y % m_orig
end

# Double - Add a point on the curve to itself.
def double(point)
  # slope = (3x^2 + a) / 2y
  slope = ((3 * point[:x] ** 2) * modinv((2 * point[:y]))) % $p # using modular inverse to perform "division"

  # new x = slope^2 - 2x
  x = (slope ** 2 - (2 * point[:x])) % $p

  # new y = slope * (x - new x) * y
  y = (slope * (point[:x] - x) - point[:y]) % $p

  # return x, y coordinates of point
  return { x: x, y: y }
end

# Add - Add two points together.
def add(point1, point2)
  # double if both points are the same
  return double(point1) if point1 == point2

  # slope = (y1 - y2) / (x1 - x2)
  slope = ((point1[:y] - point2[:y]) * modinv(point1[:x] - point2[:x])) % $p

  # new x = slope^2 - x1 - x2
  x = (slope ** 2 - point1[:x] - point2[:x]) % $p

  # new y = slope * (x1 - new x) - y1
  y = ((slope * (point1[:x] - x)) - point1[:y]) % $p

  # return x, y coordinates of point
  return { x: x, y: y }
end

# Multiply - Use the double and add operations to quickly multiply a point by an integer (e.g. a private key).
def multiply(k, point = $g) # multiply the generator point by default
  # create a copy the initial starting point (for use in addition later on)
  current = point

  # convert integer to binary representation (for use in the double and add algorithm)
  binary = k.to_s(2)

  # double and add algorithm for fast multiplication
  binary.split("").drop(1).each do |char| # ignore first binary character
    # 0 = double
    current = double(current)

    # 1 = double and add
    if char == "1"
      current = add(current, point)
    end
  end

  # return the final point
  return current
end

# -------------------------
# Private Key To Public Key
# -------------------------
# convert private key to an integer
k = private_key.to_i(16)

# multiply generator point by this private key
point = multiply(k, $g) # this point is the public key

# convert x and y values of this point to hexadecimal
x = point[:x].to_s(16).rjust(64, "0")
y = point[:y].to_s(16).rjust(64, "0")

# uncompressed public key format (not used much these days, just showing how it looks)
public_key_uncompressed = "04" + x + y

# compressed public key format (every x value has a y that could be one of two possible points)
if (point[:y] % 2 == 0)
  prefix = "02" # if y is even
else
  prefix = "03" # if y is odd
end

public_key_compressed = prefix + x # only uses the full x coordinate

# -------
# Results
# -------
puts private_key           #=> ef235aacf90d9f4aadd8c92e4b2562e1d9eb97f0df9ba3b508258739cb013db2
puts public_key_compressed #=> 02b4632d08485ff1df2db55b9dafd23347d1c47a457072a1e87be26896549a8737

Libraries

In most languages you can use an existing elliptic curve library to help you create public keys (instead of having to code the mathematics yourself). For example:

require 'ecdsa' # sudo gem install ecdsa

# This private key is just an example
privatekey = "ef235aacf90d9f4aadd8c92e4b2562e1d9eb97f0df9ba3b508258739cb013db2"

# Elliptic curve multiplication
group = ECDSA::Group::Secp256k1 # Select the curve used in Bitcoin
point = group.generator.multiply_by_scalar(privatekey.to_i(16)) # Multiply by integer (not hex)

# Convert public key point to a compressed hexadecimal public key
publickey = ECDSA::Format::PointOctetString.encode(point, compression: true).unpack("H*").join

puts publickey

Ruby: github.com/DavidEGrayson/ruby_ecdsa
PHP: github.com/BitcoinPHP/BitcoinECDSA.php

Elliptic Curve Basics

The use of elliptical curve multiplication gives you a mathematical connection from your private key to your public key.

It also has two important properties:

1. It's not known how to work backwards to get the private key.

You can go forwards using elliptic curve multiplication, but you cannot do mathematics to go backwards.

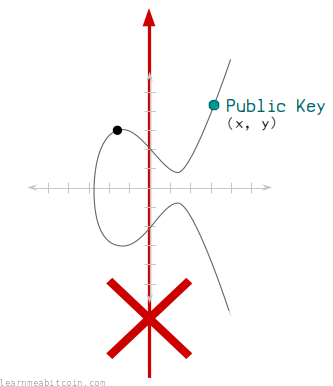
Diagram showing how you cannot work backwards to calculate a private key from a public key.

This means that there is a mathematical connection going from your private key to your public key, but nobody can use your public key to figure out what your private key is.

Therefore, you can give out your public key, but also keep your private key a secret.

2. You can prove that you have the private key without giving it away.

Basically, using some more elliptic curve mathematics, you can create a digital signature that proves that you have the corresponding private key for a public key, without ever having to give away your actual private key.

It's like saying you have the password to an account, but you don't have to show anyone your actual password to prove it.

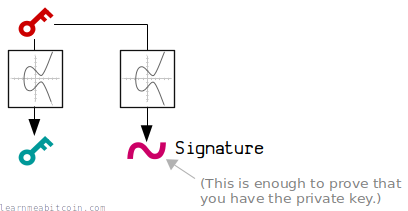
Diagram showing a signature is calculated from a private key and will also maintain a mathematical connection to the public key.

This is thanks to the magic of elliptic curve mathematics.

Formats

What does a public key look like?

A public key is just an x and y coordinate, so ultimately it's just two very large 256-bit numbers:

x: 81591541406288143274758265124625798440200740391102527151086648448953253267255
y: 64573953342291915951744135406509773051817879333910826118626860448948679381492

However, when displaying a public key we typically start by converting these numbers as two 32-byte hexadecimal values:

x: b4632d08485ff1df2db55b9dafd23347d1c47a457072a1e87be26896549a8737
y: 8ec38ff91d43e8c2092ebda601780485263da089465619e0358a5c1be7ac91f4

We then concatenate these x-y coordinates, and add a 02, 03, or 04 prefix to indicate whether we're using a compressed or uncompressed public key:

public key (uncompressed): 04b4632d08485ff1df2db55b9dafd23347d1c47a457072a1e87be26896549a87378ec38ff91d43e8c2092ebda601780485263da089465619e0358a5c1be7ac91f4
public key (compressed):   02b4632d08485ff1df2db55b9dafd23347d1c47a457072a1e87be26896549a8737

Uncompressed Public Key (legacy)

Diagram showing the format of an uncompressed public key.

An uncompressed public key is 65 bytes in length and contains the full x and y coordinates. It has an 04 byte prefix to indicate that it is an uncompressed private key.

For example:

x: b4632d08485ff1df2db55b9dafd23347d1c47a457072a1e87be26896549a8737
y: 8ec38ff91d43e8c2092ebda601780485263da089465619e0358a5c1be7ac91f4

public key (uncompressed): 04b4632d08485ff1df2db55b9dafd23347d1c47a457072a1e87be26896549a87378ec38ff91d43e8c2092ebda601780485263da089465619e0358a5c1be7ac91f4

Uncompressed public keys were used in the earliest versions of bitcoins before we figured out that we could use shorter 33-byte compressed public keys instead.

So there is no reason to use uncompressed public keys today unless you really want to or need to for some reason.

You cannot use uncompressed public keys within modern P2WPKH or P2WSH locking scripts. However, you can still use them within legacy locking scripts such as P2PK, P2PKH, P2SH, and P2MS.

Compressed Public Key

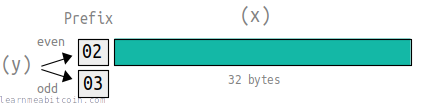
A compressed public key is 33 bytes in length. It contains the full x coordinate, and prefix to indicate whether the y coordinate is even or odd.

02 = y is even
03 = y is odd

x: b4632d08485ff1df2db55b9dafd23347d1c47a457072a1e87be26896549a8737
y: 8ec38ff91d43e8c2092ebda601780485263da089465619e0358a5c1be7ac91f4

public key (compressed): 02b4632d08485ff1df2db55b9dafd23347d1c47a457072a1e87be26896549a8737

You see, due to the structure of the elliptic curve, when you calculate the public key the y coordinate can only be one of two possible values. So instead of storing the full y coordinate, we only need to indicate which of the two possible values the y coordinate is.

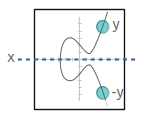
And it just so happens that the y coordinate will either be even or odd.

You should use compressed public keys by default. They're shorter (which saves space inside raw transaction data), and you avoid running into compatibility issues with modern locking scripts (e.g. P2WPKH and P2WSH only allow you to use compressed public keys).

Decompress Public Key

You can decompress a compressed public key by solving the curve equation y² = x³ + 7.

This will give you the two possible y values for the uncompressed key. You can then use the prefix from the compressed key to determine which y value to use.

# Compressed public key
compressed = "02b4632d08485ff1df2db55b9dafd23347d1c47a457072a1e87be26896549a8737"

# Split compressed key in to prefix and x-coordinate
prefix = compressed[0..1] #=> 02
x = compressed[2..-1]     #=> b4632d08485ff1df2db55b9dafd23347d1c47a457072a1e87be26896549a8737

# Convert x-coordinate from hex string to integer
x = x.to_i(16)

# Secp256k1 curve parameters
p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f # prime field

# Work out y values using the curve equation y^2 = x^3 + 7
y_sq = (x**3 + 7) % p # everything is modulo p

# Secp256k1 is chosen in a special way so that the square root of y is y^((p+1)/4)
y = y_sq.pow((p+1)/4, p) # use modular exponentiation

# Use prefix to select the correct value for y
# * 02 prefix = y is even
# * 03 prefix = y is odd
if (prefix == "02" && y % 2 != 0) # if prefix is 02 and y isn't even, use other y value
  y = (p - y) % p
end
if (prefix == "03" && y % 2 == 0) # if prefix is 03 and y is even, use other y value
  y = (p - y) % p
end

# Construct the uncompressed public key
x = x.to_s(16).rjust(64, "0") # convert to hex and make sure it's 32 bytes (64 characters)
y = y.to_s(16).rjust(64, "0")
uncompressed = "04" + x + y

# Result
puts uncompressed #=> 04b4632d08485ff1df2db55b9dafd23347d1c47a457072a1e87be26896549a87378ec38ff91d43e8c2092ebda601780485263da089465619e0358a5c1be7ac91f4

There are two possible y values due to finding the square root to solve the equation. This is because the square root of any number has two possible answers (e.g. √16=+4 or -4).

Usage

How are public keys used in Bitcoin?

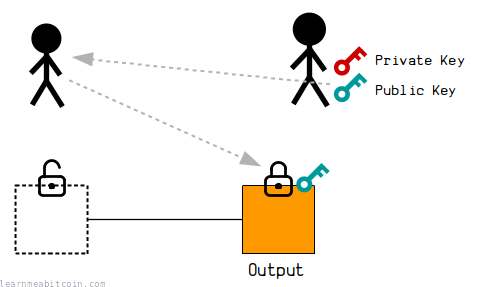
Diagram showing how you receive bitcoins when someone locks a transaction output to your public key.

A public key is used when you want to "receive" bitcoins.

When someone sends you bitcoins in a transaction, they will place your public key inside the lock on top of one of the outputs. This effectively "locks" that output to your public key, and it can only be unlocked by using the private key to create a signature that proves that you are the owner of the public key.

This is because there is a mathematical connection between the private key and the public key, and the signatures you generate using the private key will have a mathematical connection to the public key too. This mathematical connection between the public key and signature is enough to "unlock" the output for spending later on.

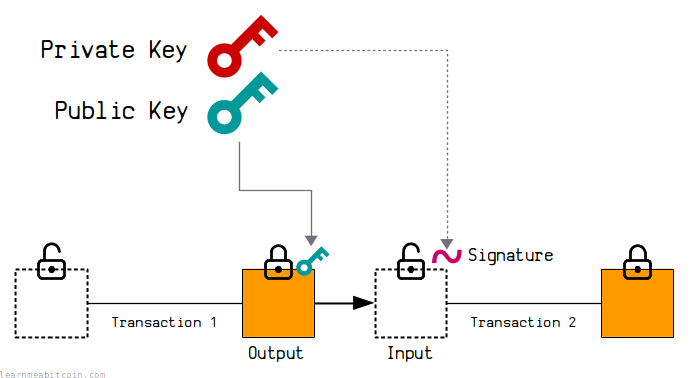
Diagram showing how keys (private key and public key) are used to lock and unlock bitcoins in transactions.

This is a simplified explanation. In the real world, the public key gets converted to an address first before sharing it with other people. However, the underlying mechanism is the same.

The following locking scripts directly lock outputs to a public key:

The following locking scripts will also typically contain a public key:

P2SH
P2WSH

Location

Where can you find public keys?

Public keys can be found inside the ScriptPubKey or ScriptSig of raw transactions.

The public key will be in a different location depending on the type of locking script placed on an output. These are some examples of typical locations of public keys inside the blockchain:

P2PK

Pay To Public Key

The public key for a P2PK is inside the ScriptPubKey on the output:

01000000010000000000000000000000000000000000000000000000000000000000000000ffffffff0804233fa04e028b12ffffffff0130490b2a010000004341047eda6bd04fb27cab6e7c28c99b94977f073e912f25d1ff7165d9c95cd9bbe6da7e7ad7f2acb09e0ced91705f7616af53bee51a238b7dc527f2be0aa60469d140ac00000000

{
  "version": "01000000",
  "inputcount": "01",
  "inputs": [
    {
      "txid": "0000000000000000000000000000000000000000000000000000000000000000",
      "vout": "ffffffff",
      "scriptsigsize": "08",
      "scriptsig": "04233fa04e028b12",
      "sequence": "ffffffff"
    }
  ],
  "outputcount": "01",
  "outputs": [
    {
      "amount": "30490b2a01000000",
      "scriptpubkeysize": "43",
      "scriptpubkey": "41047eda6bd04fb27cab6e7c28c99b94977f073e912f25d1ff7165d9c95cd9bbe6da7e7ad7f2acb09e0ced91705f7616af53bee51a238b7dc527f2be0aa60469d140ac"
    }
  ],
  "locktime": "00000000"
}

Transaction: 18a16d322b235f636ab90e62e79a9f20a0b9c14e8da51e9dc0974f99f82ee444

Note: This P2PK locking script contains an uncompressed public key.

P2PK is the simplest locking script for locking an output to a public key, as the locking script contains the public key directly.

These P2PK locking scripts are far less common than the more popular P2PKH and P2WPKH. These P2PK locking scripts are most commonly found inside early coinbase transactions between 2009 and 2011.

P2MS

Pay To Multisig

The public key(s) for a P2MS are inside the ScriptPubKey on the output:

01000000014563f26698c0ea3ebd85d4767457370d7e2ebbe922a7736dbf70e1d0f8a9aa9c000000008a473044022039294d5c8843a6776d4a2032cf03549f41c634ba5e65898c7816973919e485b902205af1f61f6d7d6a5f32cbe46676303c141fe499288b1be0d8f0c4e80d4c0ecb5701410454ffbc96ef3c26acffa431066915308865d990e044c507e0ab3d26af34a8ba5b4cb3028fe7c91926bb8be47d652dc70ab300e3022f8259db5f79306b601fc66effffffff0190c9190000000000c9524104d81fd577272bbe73308c93009eec5dc9fc319fc1ee2e7066e17220a5d47a18314578be2faea34b9f1f8ca078f8621acd4bc22897b03daa422b9bf56646b342a24104ec3afff0b2b66e8152e9018fe3be3fc92b30bf886b3487a525997d00fd9da2d012dce5d5275854adc3106572a5d1e12d4211b228429f5a7b2f7ba92eb0475bb14104b49b496684b02855bc32f5daefa2e2e406db4418f3b86bca5195600951c7d918cdbe5e6d3736ec2abf2dd7610995c3086976b2c0c7b4e459d10b34a316d5a5e753ae00000000

{
  "version": "01000000",
  "inputcount": "01",
  "inputs": [
    {
      "txid": "4563f26698c0ea3ebd85d4767457370d7e2ebbe922a7736dbf70e1d0f8a9aa9c",
      "vout": "00000000",
      "scriptsigsize": "8a",
      "scriptsig": "473044022039294d5c8843a6776d4a2032cf03549f41c634ba5e65898c7816973919e485b902205af1f61f6d7d6a5f32cbe46676303c141fe499288b1be0d8f0c4e80d4c0ecb5701410454ffbc96ef3c26acffa431066915308865d990e044c507e0ab3d26af34a8ba5b4cb3028fe7c91926bb8be47d652dc70ab300e3022f8259db5f79306b601fc66e",
      "sequence": "ffffffff"
    }
  ],
  "outputcount": "01",
  "outputs": [
    {
      "amount": "90c9190000000000",
      "scriptpubkeysize": "c9",
      "scriptpubkey": "524104d81fd577272bbe73308c93009eec5dc9fc319fc1ee2e7066e17220a5d47a18314578be2faea34b9f1f8ca078f8621acd4bc22897b03daa422b9bf56646b342a24104ec3afff0b2b66e8152e9018fe3be3fc92b30bf886b3487a525997d00fd9da2d012dce5d5275854adc3106572a5d1e12d4211b228429f5a7b2f7ba92eb0475bb14104b49b496684b02855bc32f5daefa2e2e406db4418f3b86bca5195600951c7d918cdbe5e6d3736ec2abf2dd7610995c3086976b2c0c7b4e459d10b34a316d5a5e753ae"
    }
  ],
  "locktime": "00000000"
}

Transaction: 581d30e2a73a2db683ac2f15d53590bd0cd72de52555c2722d9d6a78e9fea510

Note: This P2MS locking script contains 3 uncompressed public keys.

A P2MS allows you to lock an output to multiple public keys, and requires signatures for some or all of those public keys to unlock it.

A standard P2MS locking script can contain up to 3 public keys. Although a non-standard multisig locking script can contain up to 20 public keys at a time.

It's rare to find raw P2MS locking scripts in the blockchain, as these kind of locks are more commonly wrapped inside a P2SH instead.

P2PKH

Pay To Public Key Hash

The public key for a P2PKH is inside the ScriptSig on the input:

0200000001cc8e9c87148eae3bc918c94b13c0971d7959474e37d040c777aab7d8f621bfa2000000006a47304402204321dc44fa1207aa353ce1b0270887910c10825b284cfc5dc1e5451da43defd002204b0cab71575f765d11f52b1f03bdc3d11b00a6d94e1f2185530c6f82bdae2e7d012102e9698e55e8b3bca5aa108e094e4b0b42ce0dd697268c77ccc14ef54bd336088efeffffff02404b4c00000000001976a9148ca7043a7bf78518c3dfc9c756f3af8fef4ce6db88acc9a30a08020000001976a914b8b5866bc6828bb1e9c9ddc132fe42965355c19b88acd1bf0b00

{
  "version": "02000000",
  "inputcount": "01",
  "inputs": [
    {
      "txid": "cc8e9c87148eae3bc918c94b13c0971d7959474e37d040c777aab7d8f621bfa2",
      "vout": "00000000",
      "scriptsigsize": "6a",
      "scriptsig": "47304402204321dc44fa1207aa353ce1b0270887910c10825b284cfc5dc1e5451da43defd002204b0cab71575f765d11f52b1f03bdc3d11b00a6d94e1f2185530c6f82bdae2e7d012102e9698e55e8b3bca5aa108e094e4b0b42ce0dd697268c77ccc14ef54bd336088e",
      "sequence": "feffffff"
    }
  ],
  "outputcount": "02",
  "outputs": [
    {
      "amount": "404b4c0000000000",
      "scriptpubkeysize": "19",
      "scriptpubkey": "76a9148ca7043a7bf78518c3dfc9c756f3af8fef4ce6db88ac"
    },
    {
      "amount": "c9a30a0802000000",
      "scriptpubkeysize": "19",
      "scriptpubkey": "76a914b8b5866bc6828bb1e9c9ddc132fe42965355c19b88ac"
    }
  ],
  "locktime": "d1bf0b00"
}

Transaction: faf2987fd2240d9c46575cc35c354eeca71b794c482f3cc49fba1a5f9a80808c

Note: This P2PKH unlocking script contains a compressed public key.

With P2PKH, the initial locking script on an output (in a previous transaction) actually contains a public key hash. The actual public key is then only revealed when you come to spend the output as an input in a new transaction.

So whilst a P2PKH does the same job as a P2PK by "locking" an output to a public key, the original public key is found inside the ScriptSig (unlocking script) as opposed to the ScriptPubKey (locking script).

This was the most popular way to lock an output to a public key up until 2016 before P2WPKH was introduced in the Segregated Witness upgrade. This is because P2PKH has its own address format (which made it easier to send bitcoins when using a bitcoin wallet), whereas P2PK does not.

P2WPKH

Pay To Witness Public Key Hash

The public key for a P2WPKH is inside the Witness for the input:

020000000001013aa815ace3c5751ee6c325d614044ad58c18ed2858a44f9d9f98fbcddad878c10000000000ffffffff01344d10000000000016001430cd68883f558464ec7939d9f960956422018f0702483045022100c7fb3bd38bdceb315a28a0793d85f31e4e1d9983122b4a5de741d6ddca5caf8202207b2821abd7a1a2157a9d5e69d2fdba3502b0a96be809c34981f8445555bdafdb012103f465315805ed271eb972e43d84d2a9e19494d10151d9f6adb32b8534bfd764ab00000000

{
  "version": "02000000",
  "marker": "00",
  "flag": "01",
  "inputcount": "01",
  "inputs": [
    {
      "txid": "3aa815ace3c5751ee6c325d614044ad58c18ed2858a44f9d9f98fbcddad878c1",
      "vout": "00000000",
      "scriptsigsize": "00",
      "scriptsig": "",
      "sequence": "ffffffff"
    }
  ],
  "outputcount": "01",
  "outputs": [
    {
      "amount": "344d100000000000",
      "scriptpubkeysize": "16",
      "scriptpubkey": "001430cd68883f558464ec7939d9f960956422018f07"
    }
  ],
  "witness": [
    {
      "stackitems": "02",
      "0": {
        "size": "48",
        "item": "3045022100c7fb3bd38bdceb315a28a0793d85f31e4e1d9983122b4a5de741d6ddca5caf8202207b2821abd7a1a2157a9d5e69d2fdba3502b0a96be809c34981f8445555bdafdb01"
      },
      "1": {
        "size": "21",
        "item": "03f465315805ed271eb972e43d84d2a9e19494d10151d9f6adb32b8534bfd764ab"
      }
    }
  ],
  "locktime": "00000000"
}

Transaction: 1674761a2b5cb6c7ea39ef58483433e8735e732f5d5815c9ef90523a91ed34a6

Note: This P2WPKH unlocking code contains a compressed public key.

P2WPKH is functionally similar to P2PKH. The main difference is that the unlocking code goes inside the Witness field for the input instead of the ScriptSig.

You can only use compressed public keys with a P2WPKH.

Summary

If you've generated your own private key, the next step is to use it to calculate the corresponding public key.

This is more mathematically involved than generating the initial private key, because the private key is just a random number, but the public key requires you to use elliptic curve multiplication to calculate a specific point on the curve.

Because that's all a public key is: a pair of x and y coordinates.

It's interesting to understand how elliptic curve mathematics works, but it's not essential to be able to generate your own set of keys for use in Bitcoin. So don't be too put off by all the code and technical terms. The code isn't actually as complex as it looks, so just give it a go.

If I can figure out how to calculate one from scratch with no prior experience with cryptography, so can you.

From here, all you need to do is to be able to convert the public key into an address, and then you'll be able to start sending and receiving bitcoins using keys that you've generated all by yourself.

You can always look into the details of elliptic curves and whatnot afterwards if you want.

Good luck.

Creating

Code

Libraries

Elliptic Curve Basics

1. It's not known how to work backwards to get the private key.

2. You can prove that you have the private key without giving it away.

Formats

Uncompressed Public Key (legacy)

Compressed Public Key

Decompress Public Key

Usage

Location

P2PK

P2MS

P2PKH

P2WPKH

Summary

Resources