Hexadecimal
Numbering system using 16 symbols
Download PDF
The hexadecimal numbering system uses the digits 0-9 and the characters A-F to represent the numbers 0-15.
So basically the hexadecimal system (16 symbols) is an extension of the decimal system (10 symbols). This means you can represent numbers from 0 to 15 using just one symbol.
This system is useful for representing bytes, because half a byte has 16 different combinations, so you can represent a whole byte using just 2 hexadecimal symbols. That's why a lot of the data you see in Bitcoin (e.g. private keys, transactions) is in hexadecimal.
The letters in hexadecimal can be uppercase or lowercase, it doesn't matter (e.g. 1337af is the same as 1337AF).
Hexa = 6, Deci = 10. So hexadecimal refers to the fact that there are 16 different characters in this numbering system.
Hexadecimal to Decimal
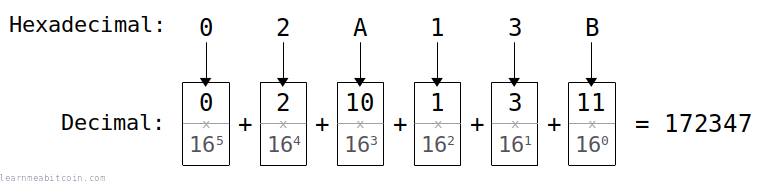
To convert hexadecimal to decimal, you multiply each character by increasing powers of 16.
- Convert each hexadecimal symbol to its corresponding decimal value.
- Multiply each of these decimal values (from smallest to largest) by an increasing power of 16 (e.g. 160, 161, 162, 163, etc.)
- Add up all of the results together to get the final decimal value.
For example:
Hexadecimal = 02A13B
B = 11 * 160 = 11
3 = 3 * 161 = 48
1 = 1 * 162 = 256
A = 10 * 163 = 40960
2 = 2 * 164 = 131072
0 = 0 * 165 = 0
Decimal = 0 + 131072 + 40960 + 256 + 48 + 11 = 172347
This sounds confusing at first, but it's exactly how the decimal system works too. Every number in a decimal value represents 10 to an increasing power (because there are 10 digits in the decimal system, aka "base 10"). For example, the number 123 is saying (1 x 102) + (2 x 101) + 3 x (100), or "one 100, two 10's, and three 1's".
Any number to the power of zero is 1. For example, 100 = 1, and 160 = 1.
You don't have to be able to convert hexadecimal to decimal in your head, but it's good to remember that ultimately you're just looking at numbers when you're looking at hexadecimal digits and characters.
Little-Endian. Most numbers stored within fields in bitcoin data (e.g. vout, amount) are in little-endian (where the bytes are in reverse order), so you need to reverse the order of bytes first before converting to decimal.
Code Examples
You can convert hexadecimal strings to decimal in any good programming language. There should be built-in functions to make it easy, so you shouldn't have to perform the conversion manually.
# hexadecimal to decimal
puts "02A13B".to_i(16) #=> 172347# hexadecimal to decimal
echo "ibase=16; 02A13B" | bc #=> 172347Decimal to Hexadecimal
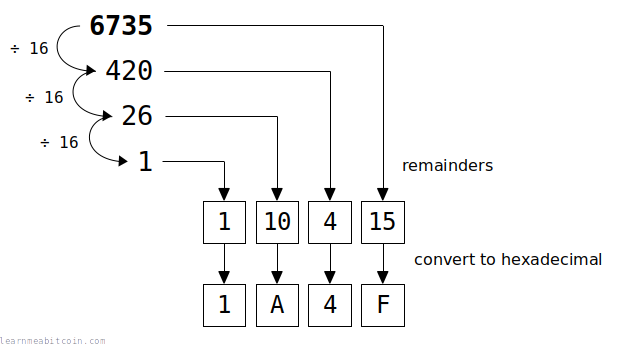
To convert decimal to hexadecimal, you just need to keep dividing by 16.
The remainder of each division gives you the number for each hexadecimal character (from smallest to largest). You then take the result of each division (quotient), and keep going until you cannot divide the remainder any more (i.e. the quotient is zero).
For example:
Decimal = 6735
6735 / 16 = 420 (remainder 15)
420 / 16 = 26 (remainder 4)
26 / 16 = 1 (remainder 10)
1 / 16 = 0 (remainder 1)
Hexadecimal = 1A4F
Modulus. The modulus operation (%) returns the remainder after division.
Code Examples
# decimal to hexadecimal
puts 6735.to_s(16) #=> 1a4f# decimal to hexadecimal
echo "obase=16; 6735" | bc #=> 1A4FBytes
What's the use of hexadecimal?
You will encounter lots of hexadecimal characters when working with raw data in Bitcoin. For example, here's a random private key:
5a14b12ee7f68f42e91d8dad1c07df82b5a030f5f28a39f65816fecf46d3ef1cThis private key represents 32 bytes of data.
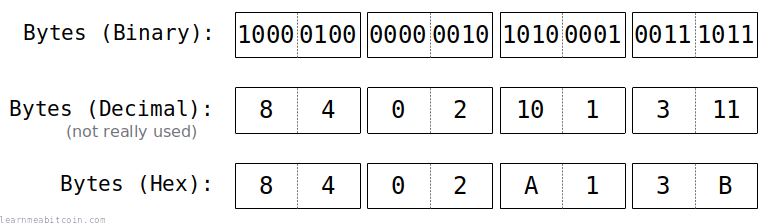
Why do we use hexadecimal for showing bytes? Because half of a byte of data has 16 different possible combinations, and there are 16 different hexadecimal characters. Therefore, we can represent half a byte using one single hexadecimal character, and a whole byte using two hexadecimal characters.
It's a match made in computing heaven.
For example, rather than displaying all eight individual bits using binary like 10110101, we can shorten it two hexadecimal characters B5 instead (because 1011 = B and 0101 = 5).
So basically, the hexadecimal system is a convenient system for displaying raw bytes of data.