HD Wallets

Hierarchical Deterministic Wallets

BIP 32: Hierarchical Deterministic Wallets

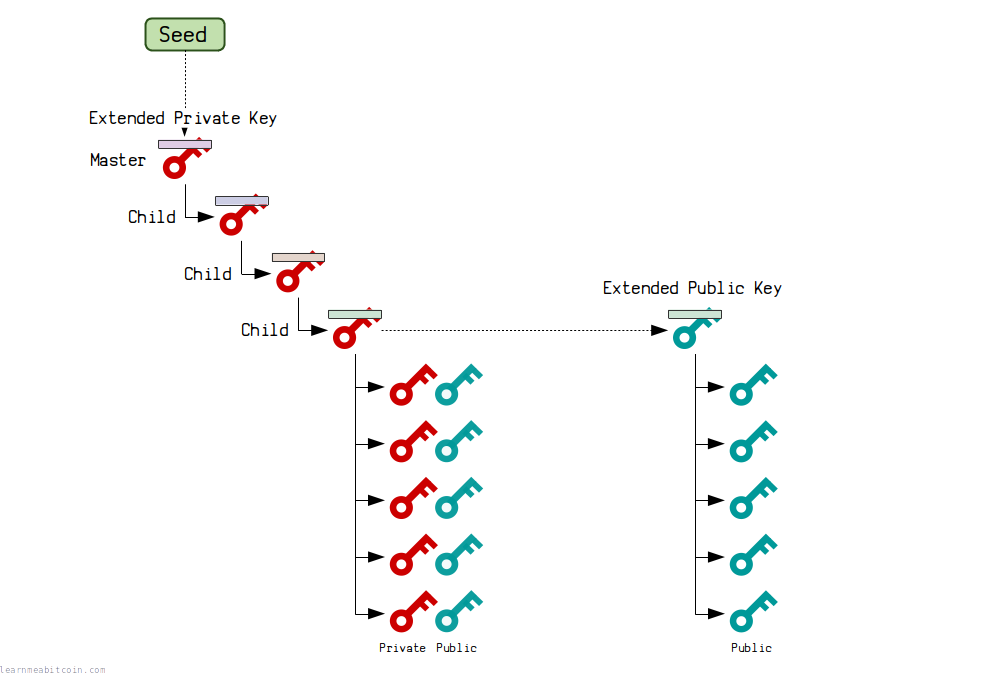
Diagram showing the basic structure of an HD Wallet.

A hierarchical deterministic wallet (or "HD Wallet") is a wallet that generates all of its keys and addresses from a single source.

So basically, an HD Wallet allows you to generate billions of private keys using a single seed. So as long as you remember the seed, you'll always be able to recover the same keys and addresses.

This makes them much more user-friendly than early bitcoin wallets that generated and stored private keys individually.

The most interesting feature of HD wallets is that you can generate new public keys without having to generate the private keys for them at the same time.

Examples

Here are some examples of popular HD wallets that I like:

Almost all modern wallets (since 2013) are hierarchical deterministic.

Mnemonic Sentence

When you create an HD wallet you will be given a 12 or 24-word mnemonic sentence. This is the source of the seed, which is then used to generate all the keys and addresses in your wallet.

For example:



  
Never use a seed generated by a website, or enter your seed into a website. Websites can easily save the seed and use it to steal all your bitcoins.






  
    
Derivation Paths

  

  
The keys in your HD wallet will be generated using one of the following derivation paths depending on the type of addresses you want to use:


  
m/44'/0'/0' <- 1addresses (P2PKH)
m/49'/0'/0' <- 3addresses (Nested-P2WPKH)
m/84'/0'/0' <- bc1addresses (P2WPKH)







Benefits


What are the benefits of a HD wallet?




1. Single backup



In a basic wallet, you would generate pairs of private keys and public keys independently each time you want to receive bitcoins.




  

    Diagram showing individual private and public keys generated in a non-HD Wallet.
    
Basic Wallet.

  




This works perfectly fine, but it means that you would need to back up your wallet every time you receive a new payment.



However, with a hierarchical deterministic wallet, you can use a single seed to create a master private key, and you can use this to generate billions of "child" private keys and public keys.




  

    Diagram showing private and public keys generated from a single seed in an HD Wallet.
    
HD Wallet (Deterministic).

  




So now all you need to back up is the seed, as the master private key you create from it will always generate the keys for your wallet in the same way (deterministically).




2. Organization



Another cool thing about hierarchical deterministic wallets is the hierarchical part.



Each child key in the wallet can also generate its own keys, which means you can create a tree structure (or hierarchy) to organize the keys in your wallet.




  

    Diagram showing the hierarchical structure of keys in an HD wallet.
    
HD Wallet (Hierarchical).

  




You then use different parts of the tree to separate the keys into different "accounts".




3. Generating public keys independently



But the really cool thing about a master private key is that it has a corresponding master public key, and this can generate the same child public keys without the private keys.




  

    Diagram showing how you can generate public keys independently of their corresponding private keys in an HD Wallet.
    
You can generate public keys independently of their corresponding private keys.

  




So you could send the master public key to a different computer (e.g. a webshop server) to generate new receiving addresses, without worrying that the private keys will get stolen if the server gets hacked.





This may seem like magic, but it's all just mathematics.



This is also useful for things like hardware wallets – you can keep your private keys on a secure device, and generate new addresses on a different computer for receiving payments.




How do HD wallets work?



The following is a visual overview of how HD wallets work.



For technical details, see extended keys.



1. Seed


Diagram showing a 64-byte seed used as the source for an HD Wallet.

To create an HD wallet, you start by generating 64 random bytes. This is our seed.




  
    
Example

  
  

    
  

  






2. Master Private Key


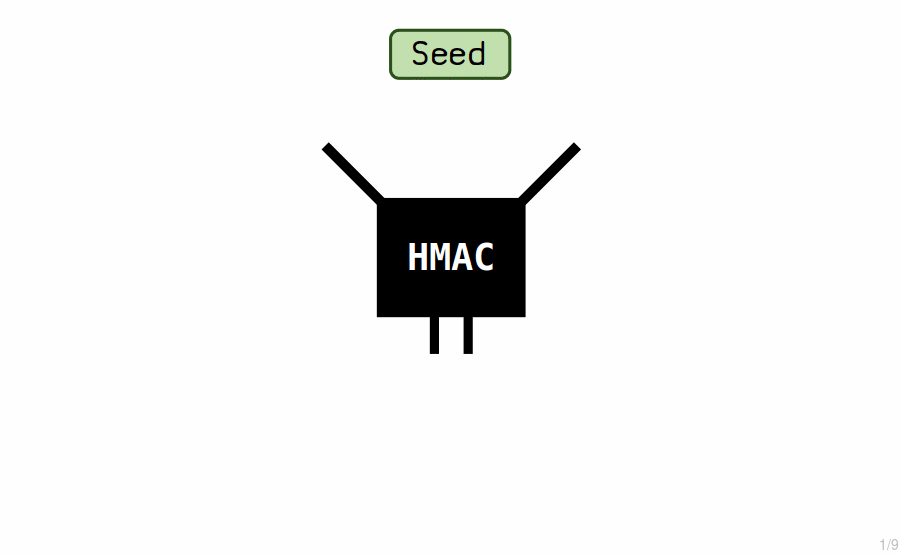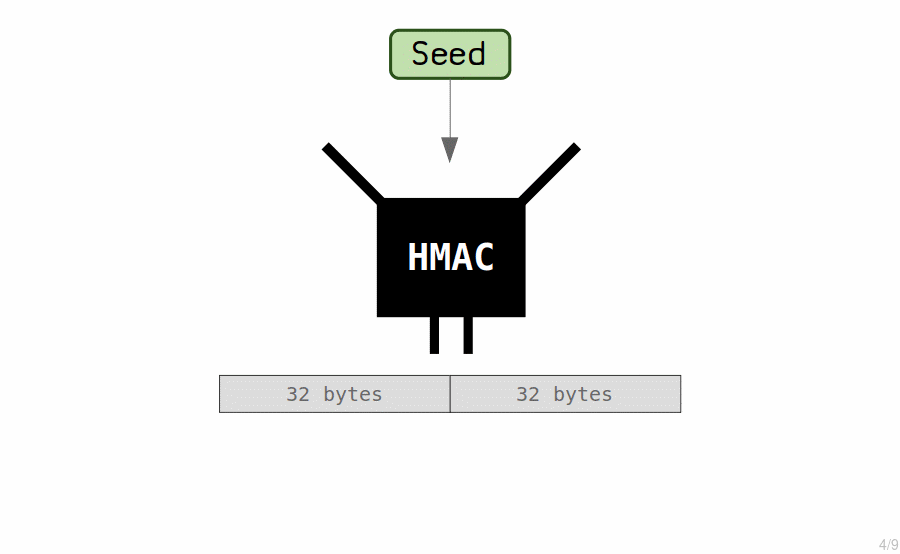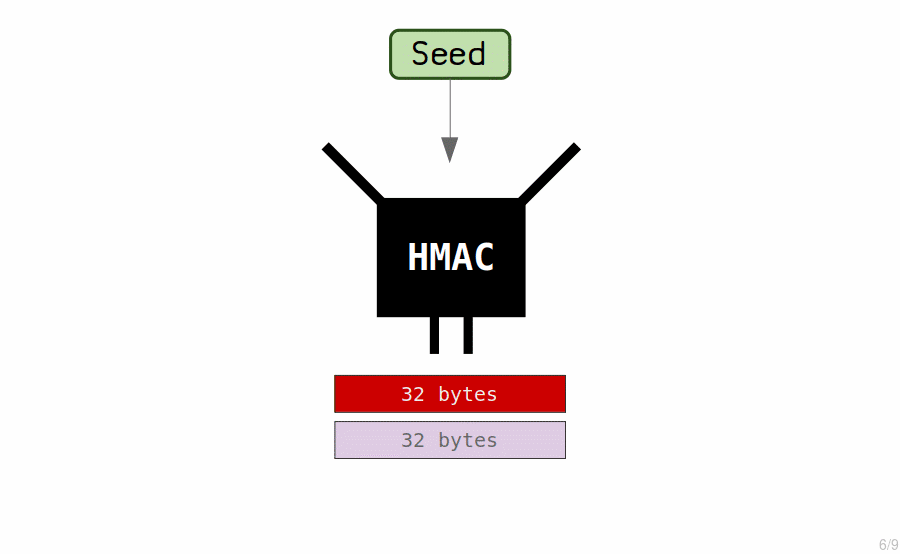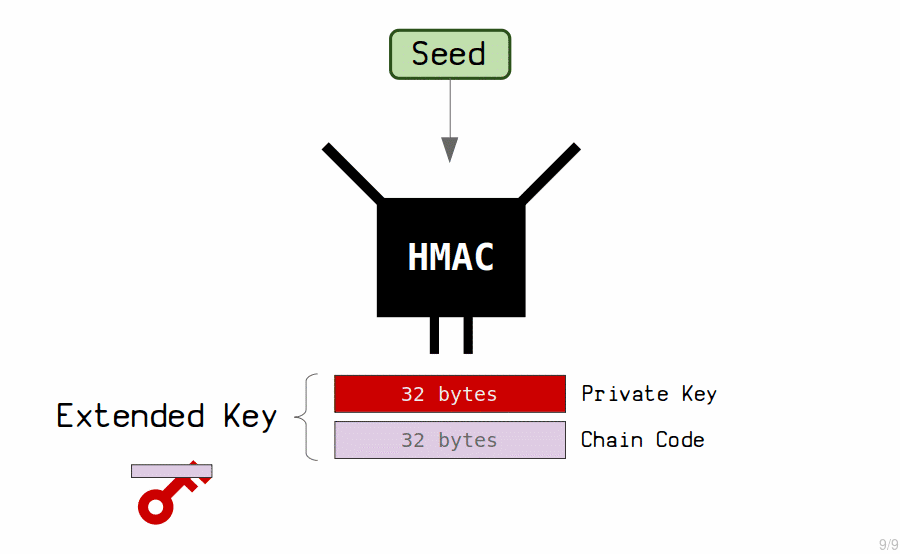
Animation showing the creation of a master private key from a 64-byte seed.

The "master key" is created by putting the seed through a hash function (called a HMAC) to generate another set of 64 bytes.



HMAC-SHA512



We use these 64 bytes to create our master extended private key.





The chain code is just an extra 32 bytes that we couple with the private key to create what we call an extended key.




  
    
Example

  
  





An "extended key" is just a normal key coupled with a chain code.



Why do we hash the seed? We could directly use the 64 byte seed to create the master extended private key. However, future child extended keys are created using the HMAC, so it's good to be consistent with how we create both.




  
The private key embedded inside an extended key can be used to create a corresponding public key as normal:


  


  
Public Key


  
The actual master extended private key itself is just the private key and chain code.






3. Child Keys (Basic)


Deriving private keys and public keys



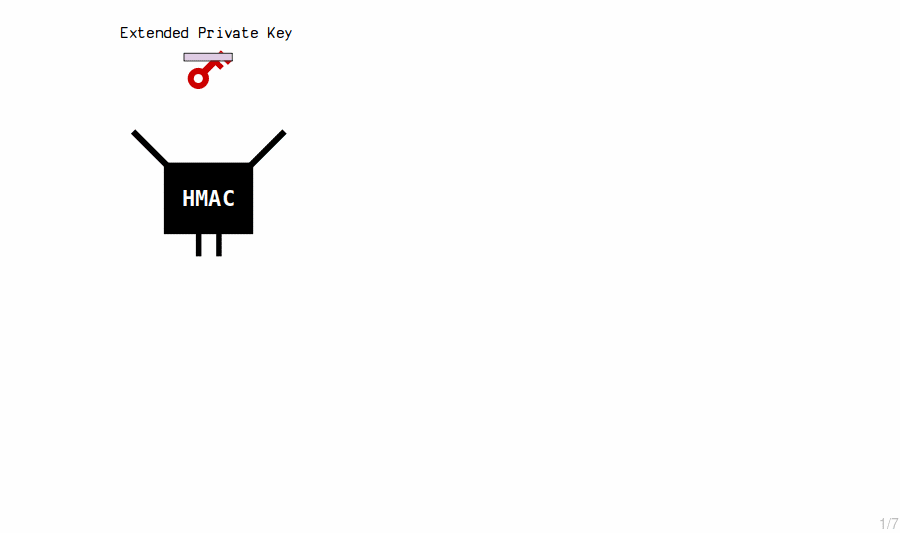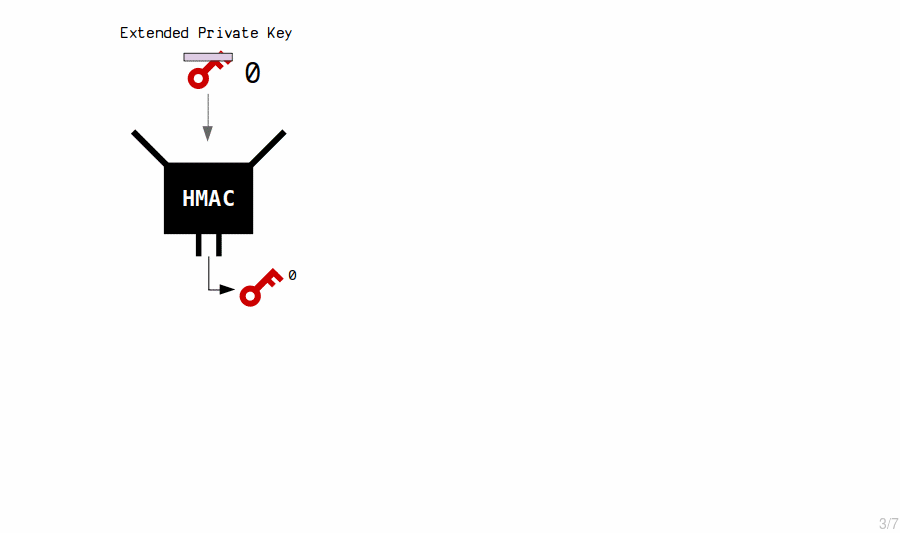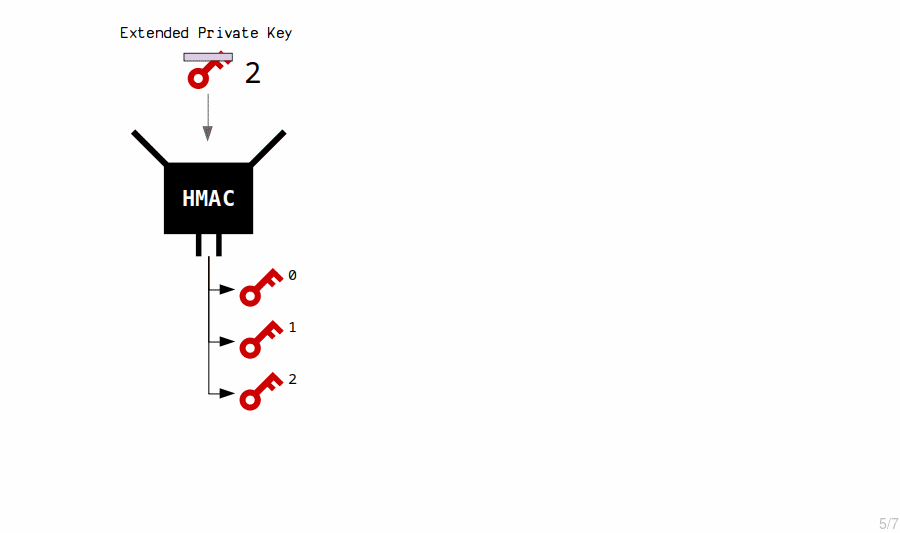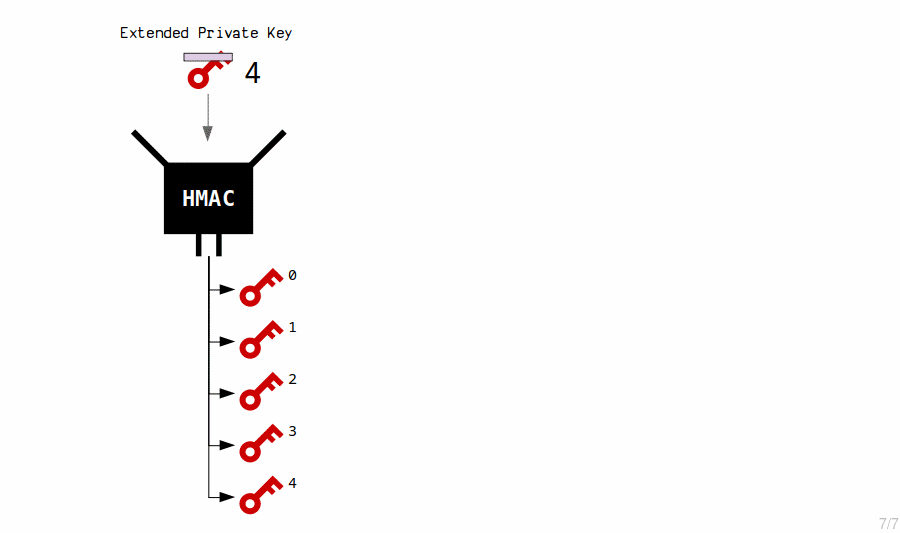
New child private keys are generated from an extended private key by putting it (the private key and chain code) through the HMAC function.



We also include an index number each time, which allows us to create multiple child keys from a single master key.




  

    Animation showing the derivation of hardened extended private key children.
    
By changing the index you get a completely different result from the hash function.

  




So essentially, new private keys are generated by hashing the master extended private key with an index number.






  
    
Example

  
  





There is an extra mathematical step when calculating the child private key after hashing the parent extended private key. So that's why you won't get the correct results by simply putting the (32-byte private key | 4-byte index) and (32-byte chain code) through the HMAC. See extended keys for details.



An extended key can generate 2,147,483,648 of these "basic" (hardened) child keys.




4. Child Keys (Advanced)


Deriving private keys and public keys, and also public keys independently



Now this is the fun part.



What if we want an extended private key to create child private keys and public keys, but also want a corresponding extended public key for it that can generate the same child public keys?



In other words, how can we generate public keys without the private keys?




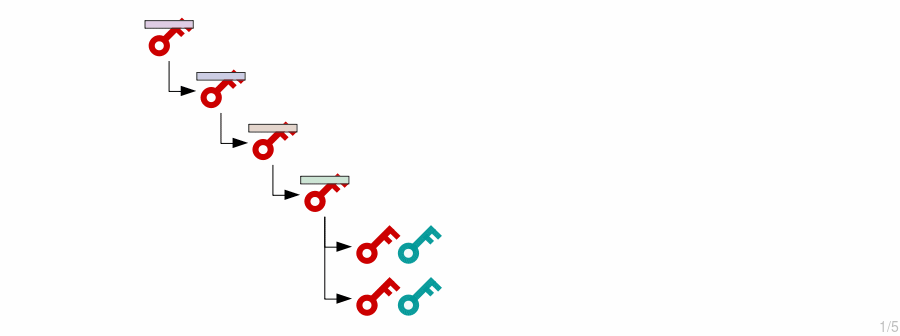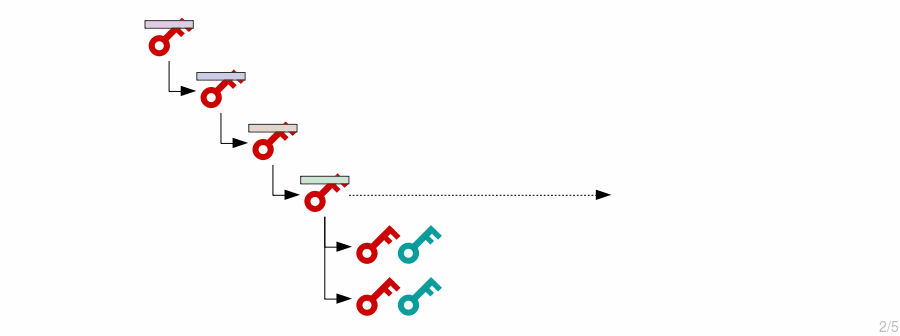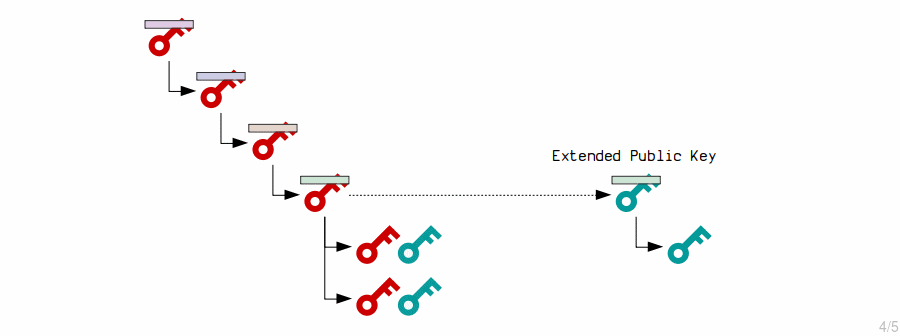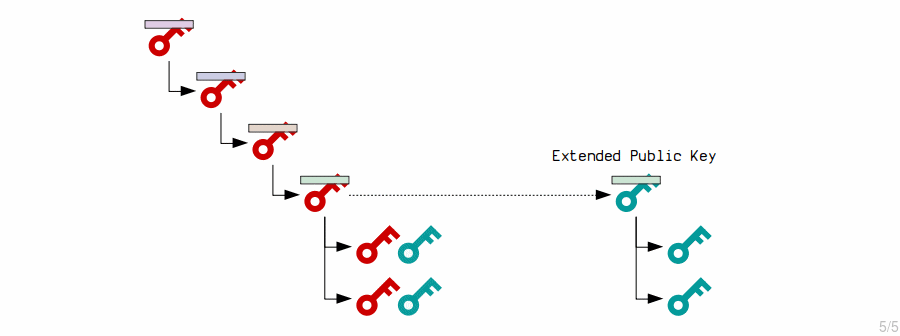
1. Extended Public Key



First, we need to construct the extended public key.



This is just the public key from the extended private key, coupled with the same chain code:


Animation showing the creation of an extended public key.

Public Key




  
    
Example

  
  








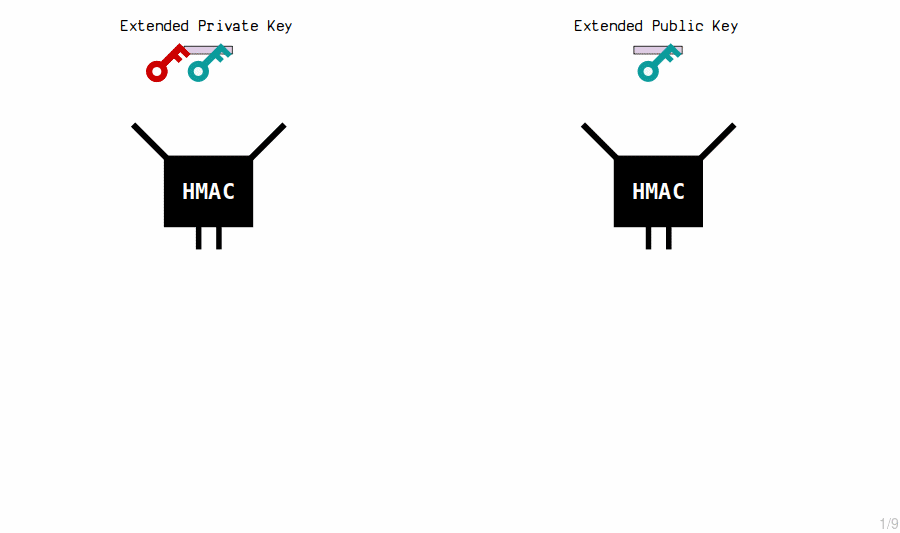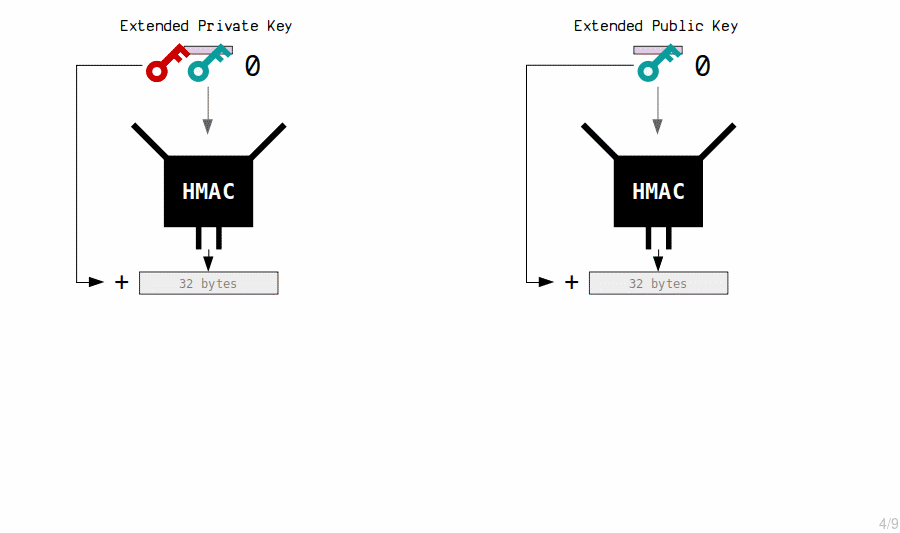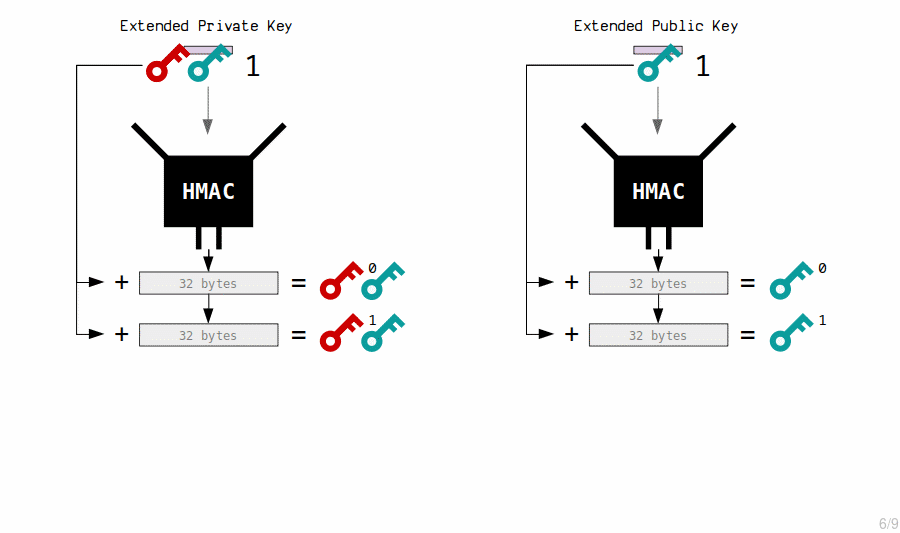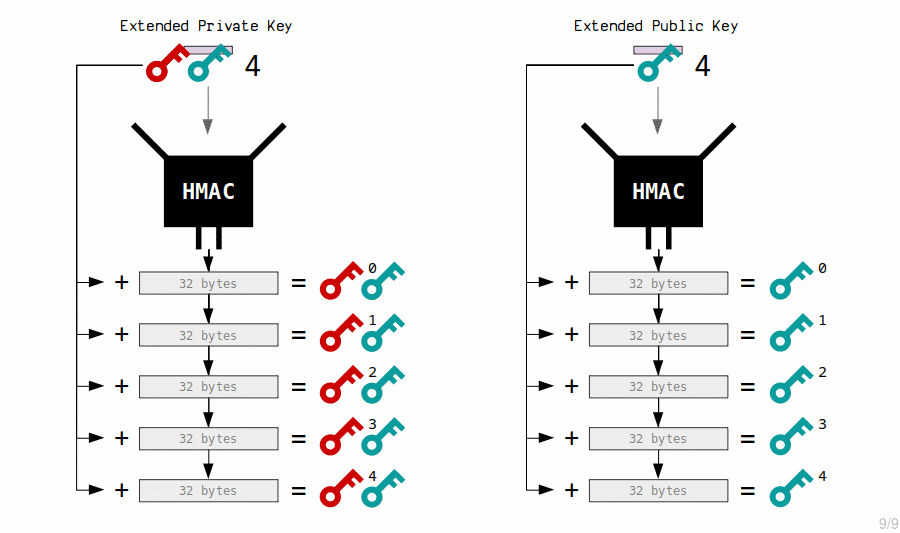
2. Extended Private Key Children



The master extended private key creates child private keys by putting the contents of its corresponding extended public key through the HMAC function, and adding the result to the original private key.


Animation showing the derivation of normal extended private key children.


  
    
Example

  
  






3. Extended Public Key Children



The master extended public key creates child public keys by putting its contents through the HMAC function, and adding the result to the original public key.


Animation showing the derivation of normal extended public key children.


  
    
Example

  
  






  




Now, because this time the child keys have been adjusted based on the parent private key and public key, the magic of elliptic curve mathematics means that the child private keys and public keys will correspond.


Animation showing the derivation of normal extended private key and extended public key children.

It seems like magic, I know, but it's just mathematics.




FAQ



Why do we use a chain code?



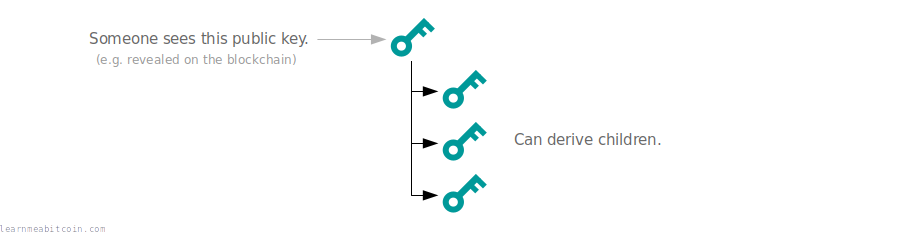
Adding a chain code means that child keys are not derived solely from the key.



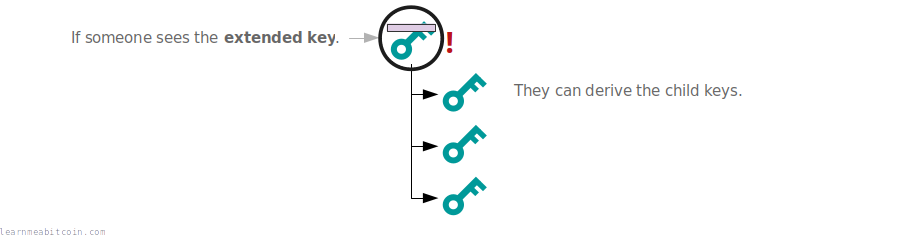
For example, we may use one of the public keys in the tree to receive a payment, which would make it visible on the blockchain. If we didn't use chain codes, anyone could take this public key and derive all the children for it:


Diagram showing how you can derive child public keys if a chain code is not used.

But by using chain codes (which do not hit the blockchain), other people are unable to derive the children from the public key:



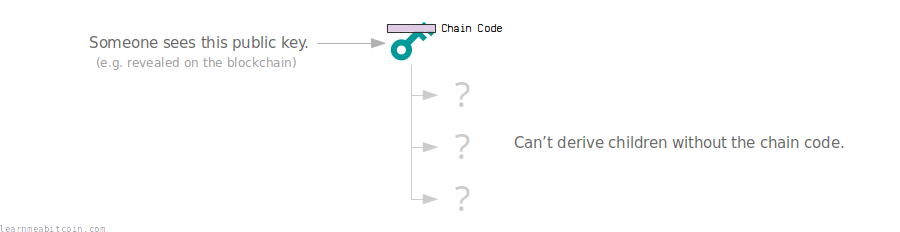
Diagram showing how you can't derive child public keys if a chain code is used.

So in other words, the chain code is additional secret data that prevents other people from deriving the children of a key.




Are the keys in an HD wallet connected?



No.



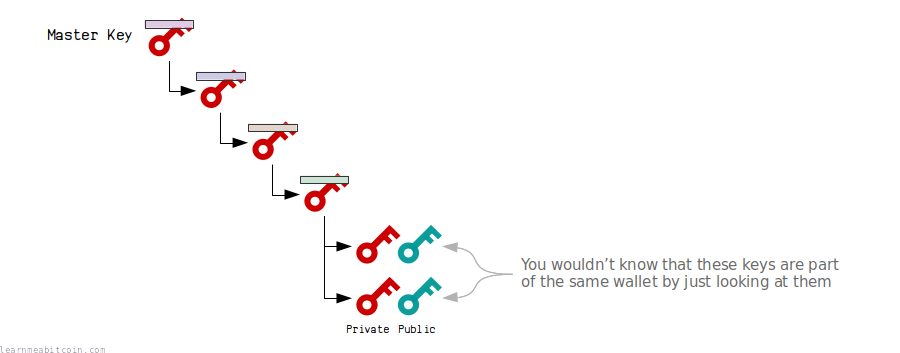
You cannot tell that any two public keys (or addresses) in the tree are part of the same wallet (i.e. derived from the same master extended key).



Even though child keys are derived from the master extended key deterministically, the actual private keys and public keys themselves do not share any resemblance to each other.



So to the outside world it's as though all the private keys and public keys were generated completely independently.


Diagram showing how the public keys in an HD wallet appear to be completely independent to the outside world.


Are the keys in an HD wallet secure?



Yes, all of the private keys and public keys you get from an HD wallet are as secure as if you generated them independently using a random number generator.



However, extended keys should be kept extra safe, as anyone who has access to them can derive all their children.



For example, if you revealed your master extended public key, other people would be able to find all the addresses in your wallet. They can't steal anything because they cannot generate the private keys for them, but they can still see how much bitcoin you own.


Diagram showing how someone can derive all the child public keys from an extended public key.


  
Leaking a parent extended public key and any child private key allows someone to calculate the parent extended private key.


  
And if they can calculate the extended private key, they can generate all the private keys at that level of the wallet (and below) and steal your bitcoins:


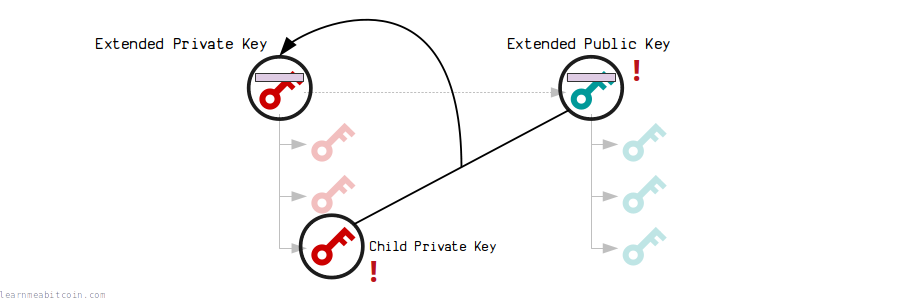
  Diagram showing how someone can derive all the child private keys from an extended public key and a single private key.
  
You might not think this would be possible at first, but it is, so be aware of it.






  





Address



The extended private keys and extended public keys in an HD wallet have their own address format.



Address (Extended Key)



For example, this is what our master extended private key looks like when serialized:






We can then make this into an address by base58check encoding it:








This is now a more useful format for our extended private key, as it's easier to share between computers and import in to wallets.



See extended key address for details.




History


Who invented HD wallets?



    
  
  1. Gregory Maxwell came up with the initial idea that you can tweak public keys to get new public keys without knowing the private keys for them, otherwise known as homomorphic derivation.
    2. 
  
  2. Armory was the first wallet to implement this homomorphic derivation, and also introduced the concept of using a chain code.
    3. 
  
  3. Pieter Wuille came up with the idea to use a hierarchical structure, and built upon the scheme used by Armory to create the BIP 32 specification.
    4. 





  
The FSF wanted to accept donations in Bitcoin and wanted to generate new addresses for each user, but didn't want their private key on their webserver.

  

    Gregory Maxwell, (on IRC)
  






  
HD wallets (BIP32) was based on Armory's scheme, but with more flexibility (the hierarchical structure), and random-access in the index (Armory's scheme required generating all N addresses before N to derivate address number n).

  

    Pieter Wuille, (on IRC)
  







Summary


Animation showing the overall structure of an HD wallet.

A hierarchical deterministic wallet provides a useful method for generating new private keys and public keys.



It's deterministic because all of the child keys are generated from a single seed in the same way each time, and it's hierarchical because you can organize the keys into a tree structure (or hierarchy). The additional benefit is that it's possible to derive the public keys in the wallet without having any knowledge of the private keys, which is pretty amazing.



Here are some more technical explanations if you're interested in the details of HD wallets:







Resources