copied
copied copied
copiedrequire 'openssl' # HMAC
require 'ecdsa' # sudo gem install ecdsa
# ----
# Seed
# ----
seed = "67f93560761e20617de26e0cb84f7234aaf373ed2e66295c3d7397e6d7ebe882ea396d5d293808b0defd7edd2babd4c091ad942e6a9351e6d075a29d4df872af"
puts "seed: #{seed}"
puts
# --------------------
# Generate Master Keys
# --------------------
# seed
# |
# m
# HMAC
hmac = OpenSSL::HMAC.hexdigest(OpenSSL::Digest::SHA512.new, "Bitcoin seed", [seed].pack("H*")) # digest, key, data
master_private_key = hmac[0..63] # left side of digest
master_chain_code = hmac[64..-1] # right side of digest
# > The SHA512-HMAC function is reused because it is already part of the standard elsewhere, but it takes a key in addition to the data being hashed.
# As the key can be arbitrary, we opted to use to make sure the key derivation was Bitcoin-specific. -- Pieter Wuille
# Get Public Key (multiply generator point by private key)
master_public_key = ECDSA::Group::Secp256k1.generator.multiply_by_scalar(master_private_key.to_i(16)) # multiply generator point by private key
master_public_key = ECDSA::Format::PointOctetString.encode(master_public_key, compression: true).unpack("H*")[0] # encode to compressed public key format
puts "master_chain_code: #{master_chain_code}" #=> 463223aac10fb13f291a1bc76bc26003d98da661cb76df61e750c139826dea8b
puts "master_private_key: #{master_private_key}" #=> f79bb0d317b310b261a55a8ab393b4c8a1aba6fa4d08aef379caba502d5d67f9
puts "master_public_key: #{master_public_key}" #=> 0252c616d91a2488c1fd1f0f172e98f7d1f6e51f8f389b2f8d632a8b490d5f6da9
puts
# --------------------------
# Child Extended Private Key
# --------------------------
# m
# |- m/0
# |- m/1
# |- m/2
# .
# .
# .
# |- m/2147483648 (hardened - m/0')
parent_private_key = master_private_key
parent_chain_code = master_chain_code
i = 0 # child number
# Normal (parent public key can create child public key for this private key)
if i < 2**31
point = ECDSA::Group::Secp256k1.generator.multiply_by_scalar(parent_private_key.to_i(16)) # multiply generator point by private key
point = ECDSA::Format::PointOctetString.encode(point, compression: true).unpack("H*")[0] # encode to compressed public key format
data = [point].pack("H*") + [i].pack("N") # point(private_key) i
end
# > This means that it is possible to give someone a parent extended key (public key + chain code), and they can derive all public keys in the chain. -- Pieter Wuille
# Hardened (parent public key cannot create public key for this private key)
if i >= 2**31
data = ["00"].pack("H*") + [parent_private_key].pack("H*") + [i].pack("N") # 0x00 private_key i
end
# > Hardened derivation should be the default unless there is a good reason why you need to be able to generate public keys without access to the private key. -- Pieter Wuille
# > You cannot derive hardened public keys from xpubs, because hardening is specifically designed to make exactly that impossible. -- Pieter Wuille
# Put data and key through hmac
key = [parent_chain_code].pack("H*") # chain code is key for hmac
hmac = OpenSSL::HMAC.hexdigest(OpenSSL::Digest::SHA512.new, key, data) # digest, key, data
il = hmac[0..63] # left side of intermediate key [32 bytes]
ir = hmac[64..-1] # right side of intermediate key [32 bytes]
# Chain code is last 32 bytes
child_chain_code = ir
if child_chain_code.to_i(16) >= ECDSA::Group::Secp256k1.order
raise "Chain code is greater than the order of the curve. Try the next index."
end
# Work out the corresponding public key too (optional)
child_private_key = (il.to_i(16) + parent_private_key.to_i(16)) % ECDSA::Group::Secp256k1.order # (il + parent_key) % n
child_private_key = child_private_key.to_s(16).rjust(64, '0') # convert to hex (and make sure it's 32 bytes long)
if child_private_key.to_i(16) == 0
raise "Child private key is zero. Try the next index."
end
child_public_key = ECDSA::Group::Secp256k1.generator.multiply_by_scalar(child_private_key.to_i(16)) # work out the public key for this too
child_public_key = ECDSA::Format::PointOctetString.encode(child_public_key, compression: true).unpack("H*")[0] # encode to compressed public key format
puts "child_chain_code: #{child_chain_code}"
puts "child_private_key: #{child_private_key}"
puts "child_public_key: #{child_public_key}"
puts
# -------------------------
# Child Extended Public Key
# -------------------------
# m -------- p
# |- p/0
# |- p/1
# |- p/3
parent_public_key = master_public_key
parent_chain_code = master_chain_code
i = 0 # child number
if i >= 2**31
raise "Can't create hardened child public keys from parent public keys."
end
key = [parent_chain_code].pack("H*")
data = [parent_public_key].pack("H*") + [i].pack("N") # 32-bit unsigned, network (big-endian) byte order
# Put data and key through hmac
hmac = OpenSSL::HMAC.hexdigest(OpenSSL::Digest::SHA512.new, key, data)
il = hmac[0..63] # left side of intermediate key [32 bytes]
ir = hmac[64..-1] # right side of intermediate key [32 bytes]
# Chain code is last 32 bytes
child_chain_code = hmac[64..-1]
if il.to_i(16) >= ECDSA::Group::Secp256k1.order
raise "Result of digest is greater than the order of the curve. Try the next index."
end
# Work out the child public key
point_hmac = ECDSA::Group::Secp256k1.generator.multiply_by_scalar(il.to_i(16)) # convert hmac il to a point
point_public = ECDSA::Format::PointOctetString.decode([parent_public_key].pack("H*"), ECDSA::Group::Secp256k1) # convert parent_public_key to a point
point = point_hmac.add_to_point(point_public) # point addition
if (point == ECDSA::Group::Secp256k1.infinity)
raise "Child public key point is at point of infinity. Try the next index."
end
child_public_key = ECDSA::Format::PointOctetString.encode(point, compression: true).unpack("H*")[0] # encode to compress public key
puts "child_chain_code: #{child_chain_code}"
puts "child_public_key: #{child_public_key}"
puts
# --------------------------
# Extended Key Serialization
# --------------------------
# Utils - Needed for creating the fingerprint and checksum, and converting hex string to Base58
# -----
require 'digest'
def create_fingerprint(parent_public_key)
hash160 = Digest::RMD160.digest(Digest::SHA256.digest([parent_public_key].pack("H*"))) # hash160 it
fingerprint = hash160[0...4].unpack("H*").join # take first 4 bytes (and convert to hex)
return fingerprint
end
def hash256(hex)
binary = [hex].pack("H*")
hash1 = Digest::SHA256.digest(binary)
hash2 = Digest::SHA256.digest(hash1)
result = hash2.unpack("H*")[0]
return result
end
def checksum(hex)
hash = hash256(hex) # Hash the data through SHA256 twice
return hash[0...8] # Return the first 4 bytes (8 characters)
end
def base58_encode(hex)
chars = %w[
1 2 3 4 5 6 7 8 9
A B C D E F G H J K L M N P Q R S T U V W X Y Z
a b c d e f g h i j k m n o p q r s t u v w x y z
]
base = chars.length
i = hex.to_i(16)
buffer = String.new
while i > 0
remainder = i % base
i = i / base
buffer = chars[remainder] + buffer
end
# add '1's to the start based on number of leading bytes of zeros
leading_zero_bytes = (hex.match(/^([0]+)/) ? $1 : '').size / 2
("1"*leading_zero_bytes) + buffer
end
# ---------
# Serialize
# ---------
parent_public_key = master_public_key # needed to create fingerprint
chain_code = child_chain_code # m/0
private_key = child_private_key # m/0
# version + depth + fingerprint + childnumber + chain_code + key + (checksum)
#
# version: puts xprv or xpub at the start
# depth: how many times this child has been derived from master key (0 = master key)
# fingerprint: created from parent public key (allows you to spot adjacent xprv and xpubs)
# childnumber: the index of this child key from the parent
# chain_code: the current chain code being used for this key
# key: the private or public key you want to create a serialized extended key for (prepend 0x00 for private)
version = "0488ade4" # private = 0x0488ade4 (xprv), public = 0x0488b21e (xpub)
depth = "01"
fingerprint = create_fingerprint(parent_public_key) #=> "018c1259"
childnumber = "00000000" # 4 byte hexadecimal string
chain_code = chain_code
key = "00" + private_key # prepend 00 to private keys (to make them 33 bytes, the same as public keys)
serialized = version + depth + fingerprint + childnumber + chain_code + key
extended_private_key = base58_encode(serialized + checksum(serialized))
puts "extended_private_key: #{extended_private_key}"
Extended Keys
Keys that can derive new keys
An extended key is a private key or public key that can be used derive new keys in an HD wallet.
Therefore, you can have a single extended private key, and use it as the source for all the child private keys and public keys in your wallet.
Furthermore, an extended private key can have a corresponding extended public key, which can be used generate the same child public keys only.
Master Extended Key
The master extended key is the first extended key in a wallet. It's created by putting a seed through the HMAC-SHA512 hash function.
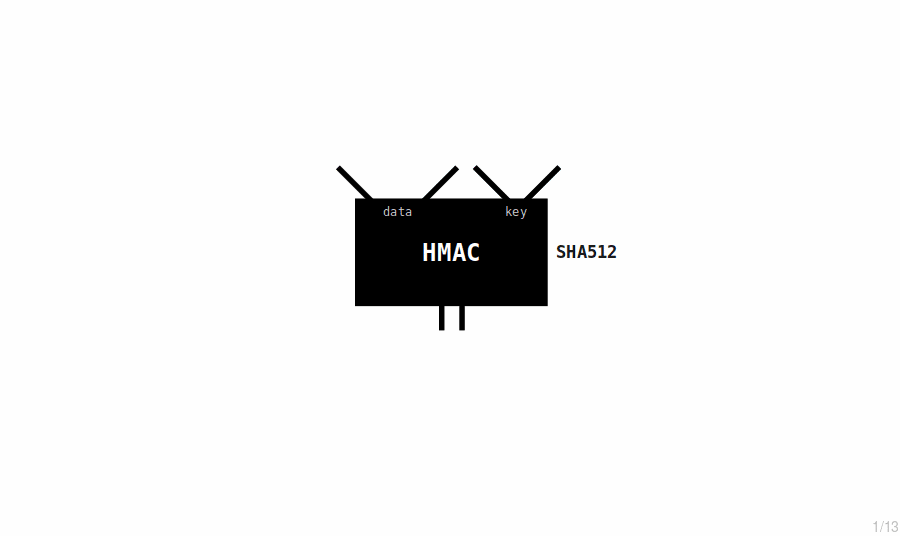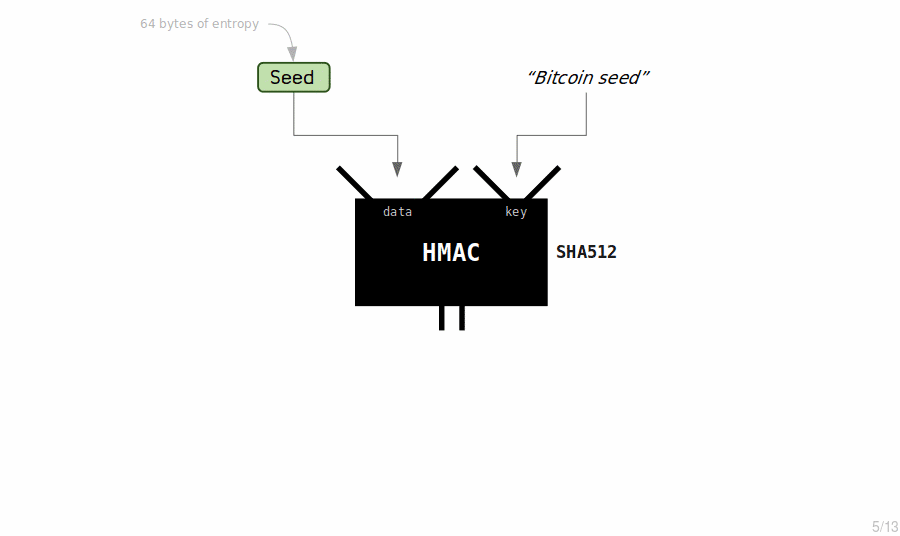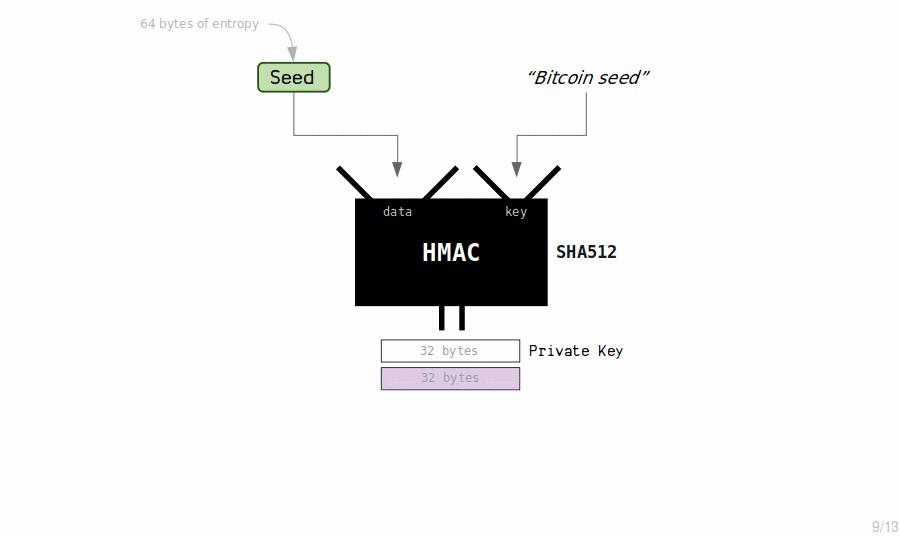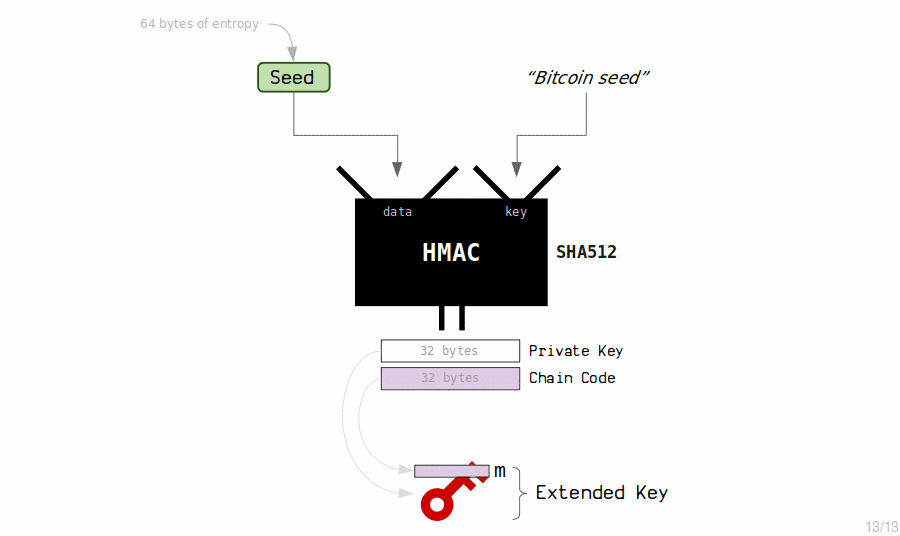
The HMAC function returns 64 bytes of data (which is totally unpredictable). We split this in to two halves to create our master extended private key:
- The first half will be the private key, which is just like any other private key.
- The second half will be the chain code, which is just an extra 32 bytes of secret data.
- HMAC is a hashing method that allows you to pass in data along with an additional secret key to produce a new set of random bytes.
- The reason we hash the seed through HMAC-SHA512 to get a 64 byte result (even though the seed is already 64 bytes) is because the seed could have been between 128 and 512 bits (16 and 64 bytes) in the original BIP 32 specification (2012). However, this step is a bit redundant now, because since BIP 39 (2013) all seeds generated from a mnemonic sentence will already be 64 bytes.
- The chain code is required for generating child keys. If you got hold of the private key but not the chain code, you wouldn't be able to derive the descendant keys (thereby protecting them).
And there we have our master extended private key and master extended public key.
Extended keys are nothing special – they're just a set of normal keys that share the same chain code (an extra 32 bytes of secret data). The real magic of extended keys is how we generate their children.
Code

 copied
copied copied
copiedrequire 'openssl' # HMAC
require 'ecdsa' # sudo gem install ecdsa
# ----
# Seed
# ----
seed = "67f93560761e20617de26e0cb84f7234aaf373ed2e66295c3d7397e6d7ebe882ea396d5d293808b0defd7edd2babd4c091ad942e6a9351e6d075a29d4df872af"
puts "seed: #{seed}"
puts
# --------------------
# Generate Master Keys
# --------------------
# seed
# |
# m
# HMAC
hmac = OpenSSL::HMAC.hexdigest(OpenSSL::Digest::SHA512.new, "Bitcoin seed", [seed].pack("H*")) # digest, key, data
master_private_key = hmac[0..63] # left side of digest
master_chain_code = hmac[64..-1] # right side of digest
# > The SHA512-HMAC function is reused because it is already part of the standard elsewhere, but it takes a key in addition to the data being hashed.
# As the key can be arbitrary, we opted to use to make sure the key derivation was Bitcoin-specific. -- Pieter Wuille
# Get Public Key (multiply generator point by private key)
master_public_key = ECDSA::Group::Secp256k1.generator.multiply_by_scalar(master_private_key.to_i(16)) # multiply generator point by private key
master_public_key = ECDSA::Format::PointOctetString.encode(master_public_key, compression: true).unpack("H*")[0] # encode to compressed public key format
puts "master_chain_code: #{master_chain_code}" #=> 463223aac10fb13f291a1bc76bc26003d98da661cb76df61e750c139826dea8b
puts "master_private_key: #{master_private_key}" #=> f79bb0d317b310b261a55a8ab393b4c8a1aba6fa4d08aef379caba502d5d67f9
puts "master_public_key: #{master_public_key}" #=> 0252c616d91a2488c1fd1f0f172e98f7d1f6e51f8f389b2f8d632a8b490d5f6da9
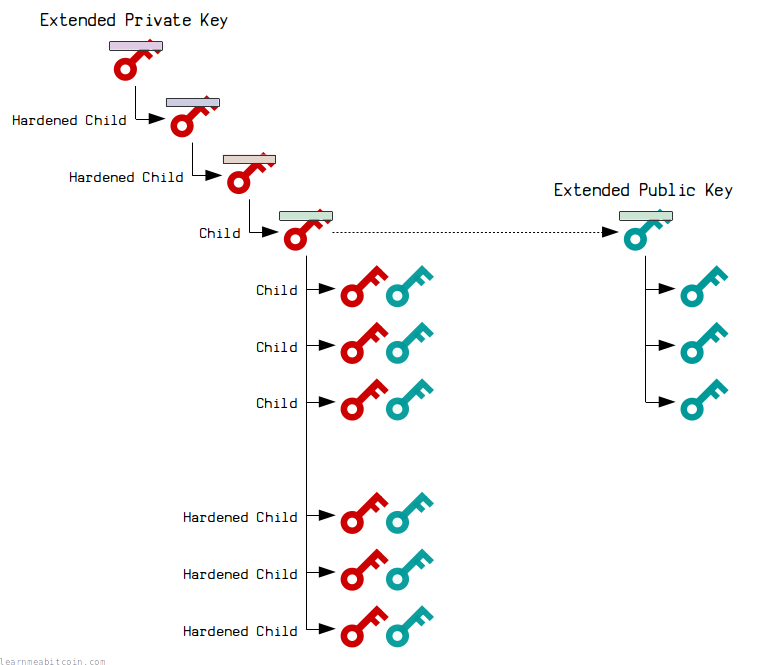
Extended Key Tree
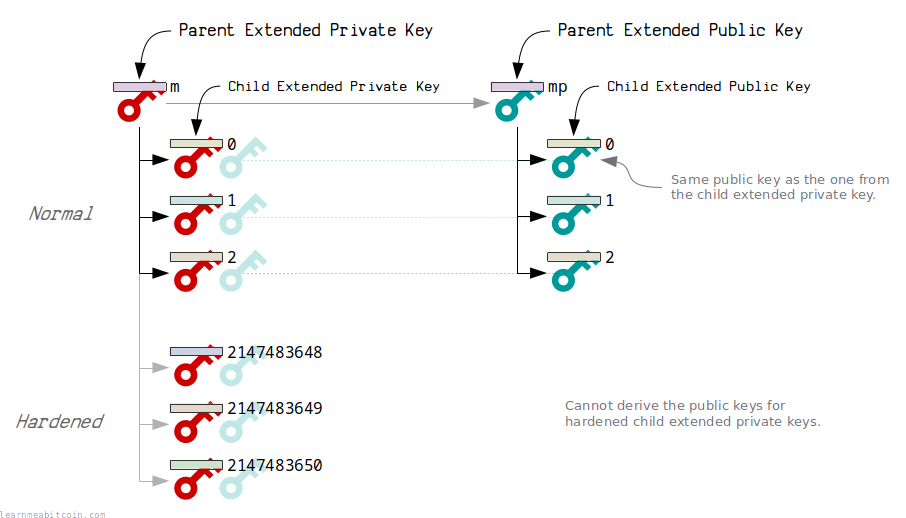
All extended keys can derive child extended keys.
- extended private keys can generate child keys with new private keys and public keys.
- extended public keys can generate child keys with new public keys only.
Each child also has an index number up to 4294967295 (which is the largest 4-byte number).
For security, you can derive two types of children from an extended private key:
- Normal – The extended private key and extended public key can generate the same public key.
Indexes 0 to 2147483647 (the first half of all possible children) - Hardened – Only the extended private key can generate the public key.
Indexes 2147483648 to 4294967295 (the second half of all possible children)
In other words, a hardened child gives you the option of creating a "secret" or "internal" public key, as they cannot be derived from an extended public key.
Hardened derivation should be the default unless there is a good reason why you need to be able to generate public keys without access to the private key.
The fact that the extended public key can generate the same public keys as the extended private key is what makes them useful.
Child Key Derivation
Both extended private keys and extended public keys can derive children, each with their own unique index number.
There are 3 methods for deriving child keys:
- Extended Private Key (Normal Child)
- Extended Private Key (Hardened Child)
- Extended Public Key (Normal Child)
It's not possible to derive a hardened extended public key.
Derived child extended keys are independent of each other. In other words, you wouldn't know that two public keys in a wallet (i.e. an extended key tree) are connected in any way.
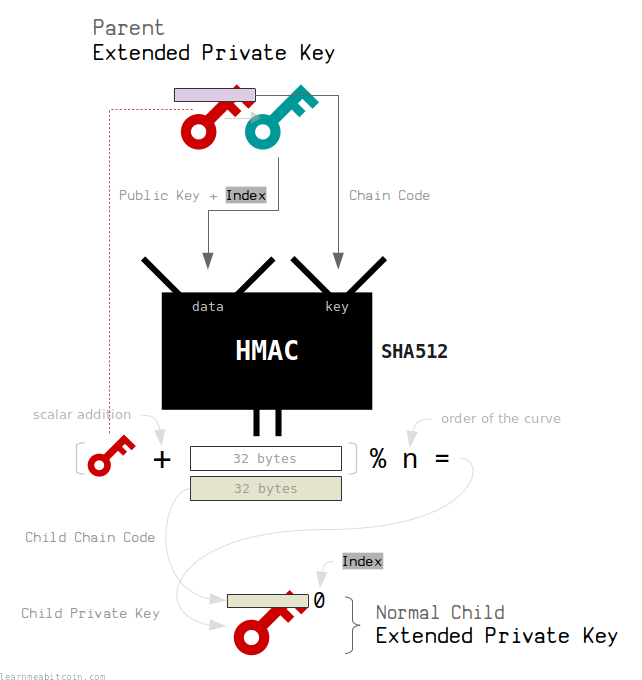
Extended Private Key (Normal Child)
A normal child extended private key is created from a parent extended private key using the following steps:
- Work out the public key for the parent extended private key.
This is important, because the corresponding extended public key will put the same data into the HMAC function when deriving their children. - Use an index between 0 and 2147483647.
Indexes in this range are designated for normal child extended keys. - Put data and key through HMAC:
- data = 33-byte public key | 4-byte index (concatenated)
- key = 32-byte chain code
The child chain code is the last 32 bytes of the result from the HMAC. This is just a unique set of bytes that we can use for the new chain code.
The child private key is the first 32 bytes of the result from the HMAC added to the parent private key. This essentially just takes the original private key and increases it by a random 32-byte number. We also modulo the child private key by the order of the curve to keep the new private key within the valid range of numbers for the elliptic curve.
So in summary, we use the data inside the parent extended private key (public key+index, chain code) and put it through the HMAC function to produce some new random bytes. We use these new random bytes to construct the child private key and chain code.
We can produce completely different child extended keys just by changing the index. Changing the index number changes the input into the HMAC, and therefore completely changes the result.
Code

 copied
copied copied
copiedrequire 'openssl' # HMAC
require 'ecdsa' # sudo gem install ecdsa
# ---------------------------------
# Normal Child Extended Private Key
# ---------------------------------
# m
# |- m/0
# |- m/1
# |- m/2
# ...
parent_chain_code = "463223aac10fb13f291a1bc76bc26003d98da661cb76df61e750c139826dea8b"
parent_private_key = "f79bb0d317b310b261a55a8ab393b4c8a1aba6fa4d08aef379caba502d5d67f9"
parent_public_key = "0252c616d91a2488c1fd1f0f172e98f7d1f6e51f8f389b2f8d632a8b490d5f6da9"
i = 0 # child index number
# Prepare data and key to put through HMAC function
data = [parent_public_key].pack("H*") + [i].pack("N") # public key + index
key = [parent_chain_code].pack("H*") # chain code is key for hmac
hmac = OpenSSL::HMAC.hexdigest(OpenSSL::Digest::SHA512.new, key, data) # digest, key, data
il = hmac[0..63] # left side of intermediate key [32 bytes]
ir = hmac[64..-1] # right side of intermediate key [32 bytes]
# Chain code is last 32 bytes
child_chain_code = ir
# Check the chain code is valid.
if child_chain_code.to_i(16) >= ECDSA::Group::Secp256k1.order
raise "Chain code is greater than the order of the curve. Try the next index."
end
# Calculate child private key
child_private_key = (il.to_i(16) + parent_private_key.to_i(16)) % ECDSA::Group::Secp256k1.order # (il + parent_key) % n
child_private_key = child_private_key.to_s(16).rjust(64, '0') # convert to hex (and make sure it's 32 bytes long)
# Work out the corresponding public key too (optional)
child_public_key = ECDSA::Group::Secp256k1.generator.multiply_by_scalar(child_private_key.to_i(16)) # work out the public key for this too
child_public_key = ECDSA::Format::PointOctetString.encode(child_public_key, compression: true).unpack("H*")[0] # encode to compressed public key format
# Results
puts "child_chain_code: #{child_chain_code}" #=> 05aae71d7c080474efaab01fa79e96f4c6cfe243237780b0df4bc36106228e31
puts "child_private_key: #{child_private_key}" #=> 39f329fedba2a68e2a804fcd9aeea4104ace9080212a52ce8b52c1fb89850c72
puts "child_public_key: #{child_public_key}" #=> 030204d3503024160e8303c0042930ea92a9d671de9aa139c1867353f6b6664e59
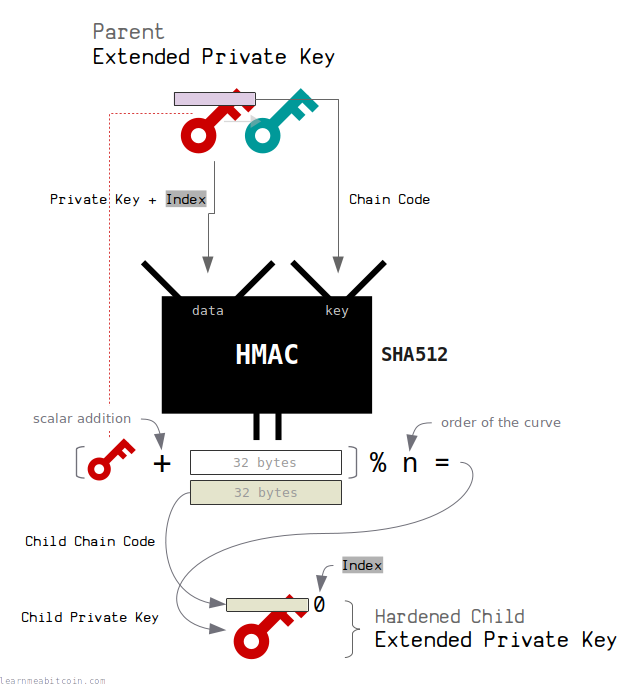
Extended Private Key (Hardened Child)
A hardened child extended private key is created from a parent extended private key using the following steps:
- Use an index between 2147483648 and 4294967295.
Indexes in this range are designated for hardened child extended keys. - Put data and key through HMAC:
- data = 0x00 | 32-byte private key | 4-byte index (concatenated)
Note: Don't forget the 0x00 byte prefix. This distinguishes it as a private key and makes the data the same length as when a public key is used instead. - key = 32-byte chain code
- data = 0x00 | 32-byte private key | 4-byte index (concatenated)
The child chain code is the last 32 bytes of the result from the HMAC.
The child private key is the first 32 bytes of the result from the HMAC added to the parent private key. This again just takes the original private key and increases it by a random 32-byte number.
Notice that this hardened child extended private key was constructed by putting the parent private key (instead of the parent public key) into the HMAC function, which an extended public key does not have access to.
As a result, hardened child extended private keys have public keys that cannot be derived by a corresponding extended public key.
Code

 copied
copied copied
copiedrequire 'openssl' # HMAC
require 'ecdsa' # sudo gem install ecdsa
# -----------------------------------
# Hardened Child Extended Private Key
# -----------------------------------
# m
# ...
# |- m/2147483648
# |- m/2147483649
# |- m/2147483650
# ...
parent_chain_code = "463223aac10fb13f291a1bc76bc26003d98da661cb76df61e750c139826dea8b"
parent_private_key = "f79bb0d317b310b261a55a8ab393b4c8a1aba6fa4d08aef379caba502d5d67f9"
i = 2147483648 # child index number (must between 2**31 and 2**32-1)
# Prepare data and key to put through HMAC function
data = ["00"].pack("H*") + [parent_private_key].pack("H*") + [i].pack("N") # 0x00 + private_key + index
key = [parent_chain_code].pack("H*") # chain code is key for hmac
hmac = OpenSSL::HMAC.hexdigest(OpenSSL::Digest::SHA512.new, key, data) # digest, key, data
il = hmac[0..63] # left side of intermediate key [32 bytes]
ir = hmac[64..-1] # right side of intermediate key [32 bytes]
# Chain code is last 32 bytes
child_chain_code = ir
# Check the chain code is valid.
if child_chain_code.to_i(16) >= ECDSA::Group::Secp256k1.order
raise "Chain code is greater than the order of the curve. Try the next index."
end
# Calculate child private key
child_private_key = (il.to_i(16) + parent_private_key.to_i(16)) % ECDSA::Group::Secp256k1.order # (il + parent_key) % n
child_private_key = child_private_key.to_s(16).rjust(64, '0') # convert to hex (and make sure it's 32 bytes long)
# Work out the corresponding public key too (optional)
child_public_key = ECDSA::Group::Secp256k1.generator.multiply_by_scalar(child_private_key.to_i(16)) # work out the public key for this too
child_public_key = ECDSA::Format::PointOctetString.encode(child_public_key, compression: true).unpack("H*")[0] # encode to compressed public key format
puts "child_chain_code: #{child_chain_code}" #=> cb3c17166cc30eb7fdd11993fb7307531372e565cd7c7136cbfa4655622bc2be
puts "child_private_key: #{child_private_key}" #=> 7272904512add56fef94c7b4cfc62bedd0632afbad680f2eb404e95f2d84cbfa
puts "child_public_key: #{child_public_key}" #=> 0355cff4a963ce259b08be9a864564caca210eb4eb35fcb75712e4bba7550efd95
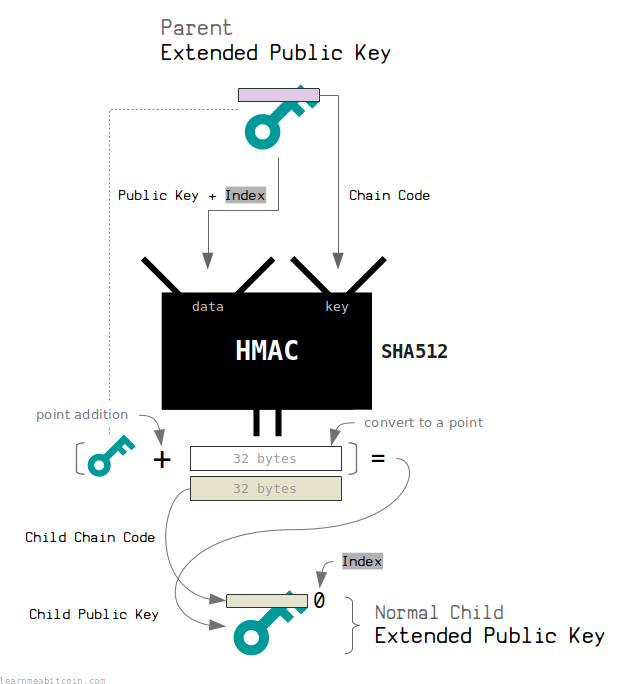
Extended Public Key (Normal Child)
A normal child extended public key is created from a parent extended public key using the following steps:
- Use an index between 0 and 2147483647.
Indexes in this range are designated for normal child extended keys. - Put data and key through HMAC.
- data = 33-byte public key + 4-byte index (concatenated)
- key = 32-byte chain code
The child chain code is the last 32 bytes of the result from the HMAC. This will be the same chain code as the normal child extended private key above, because if you look back you'll see that we put the same inputs into the HMAC function.
The child public key is the parent public key point added to another point on the curve created from the first 32 bytes of the result of the HMAC (you multiply this by the generator point to get this as a point).
So in summary, we put the same data and key into the HMAC function as we did when generating the normal child extended private key.
The child public key is then calculated via elliptic curve point addition using the same first 32 bytes of the HMAC result (which means it will actually correspond to the private key in the child extended private key).
Code

 copied
copied copied
copiedrequire 'openssl' # HMAC
require 'ecdsa' # sudo gem install ecdsa
# --------------------------------
# Normal Child Extended Public Key
# --------------------------------
# m -------- p
# |- p/0
# |- p/1
# |- p/3
parent_chain_code = "463223aac10fb13f291a1bc76bc26003d98da661cb76df61e750c139826dea8b"
parent_public_key = "0252c616d91a2488c1fd1f0f172e98f7d1f6e51f8f389b2f8d632a8b490d5f6da9"
i = 0 # child index number
if i >= 2**31
raise "Can't create hardened child public keys from parent public keys."
end
# Prepare data and key to put through HMAC function
key = [parent_chain_code].pack("H*")
data = [parent_public_key].pack("H*") + [i].pack("N") # 32-bit unsigned, network (big-endian) byte order
hmac = OpenSSL::HMAC.hexdigest(OpenSSL::Digest::SHA512.new, key, data)
il = hmac[0..63] # left side of intermediate key [32 bytes]
ir = hmac[64..-1] # right side of intermediate key [32 bytes]
# Chain code is last 32 bytes
child_chain_code = hmac[64..-1]
if il.to_i(16) >= ECDSA::Group::Secp256k1.order
raise "Result of digest is greater than the order of the curve. Try the next index."
end
# Work out the child public key
point_hmac = ECDSA::Group::Secp256k1.generator.multiply_by_scalar(il.to_i(16)) # convert hmac il to a point
point_public = ECDSA::Format::PointOctetString.decode([parent_public_key].pack("H*"), ECDSA::Group::Secp256k1) # convert parent_public_key to a point
point = point_hmac.add_to_point(point_public) # point addition
if (point == ECDSA::Group::Secp256k1.infinity)
raise "Child public key point is at point of infinity. Try the next index."
end
child_public_key = ECDSA::Format::PointOctetString.encode(point, compression: true).unpack("H*")[0] # encode to compress public key
puts "child_chain_code: #{child_chain_code}"
puts "child_public_key: #{child_public_key}"
Extended Public Key (Hardened Child)
Not possible.
Mathematics
How do extended keys work?
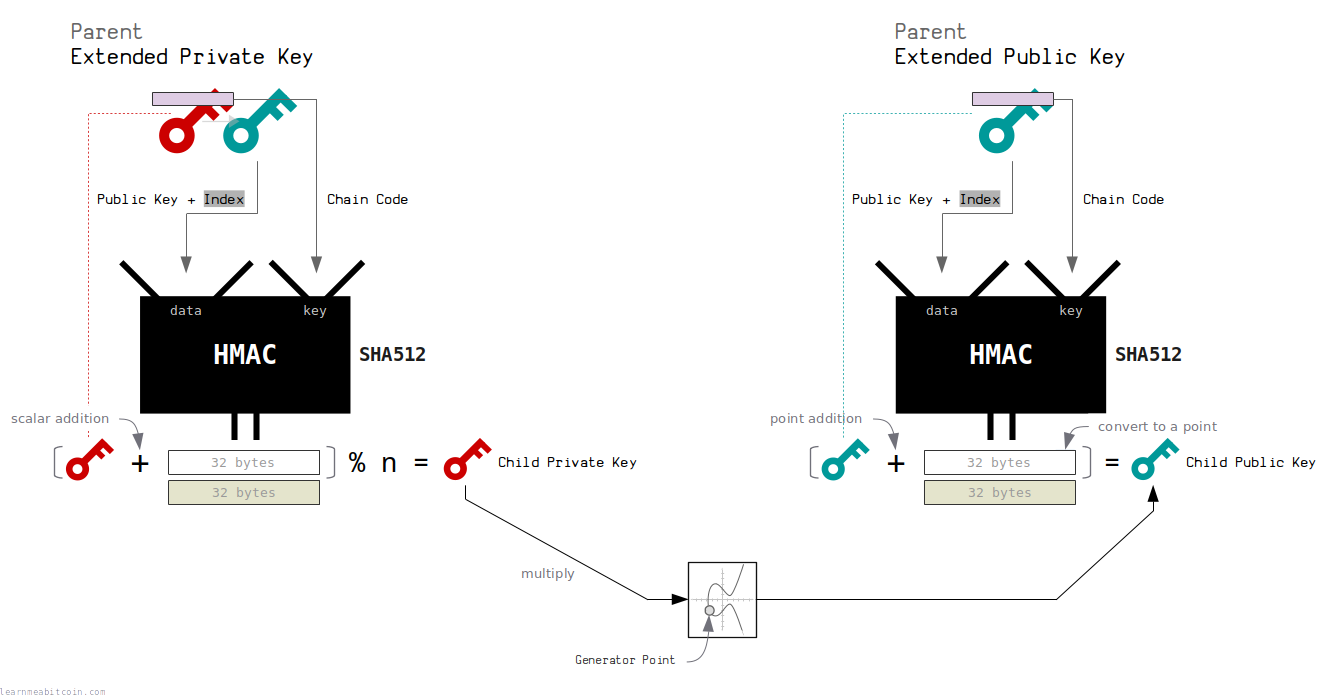
In other words, how is it possible that a public key derived from an extended public key corresponds to a private key derived from an extended private key?
Basic
Well, for both child extended keys, we are putting the same inputs in the HMAC function, so we're getting the same data as a result. Using the first 32 bytes of this data (which is basically a number) we then:
- Increase the parent private key by this number to create the child private key.
- Increase the parent public key by the same amount to create the child public key.
And due to the way elliptic curve mathematics works, the child private key will correspond to the child public key.
Technical
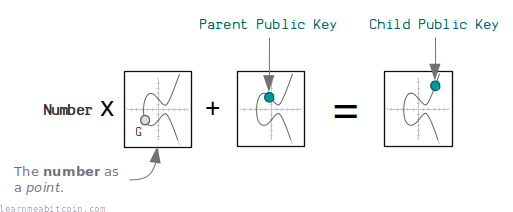
First of all, remember that a public key is just the generator point on an elliptic curve multiplied by a private key:
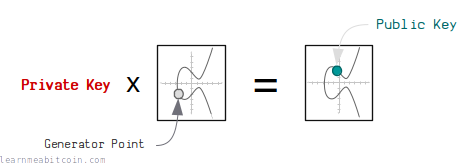
Now, if you increase this parent private key by a number (i.e. the first 32 bytes of the HMAC result) we get a new child private key. When you multiply this child private key by the generator point, we get the child public key:
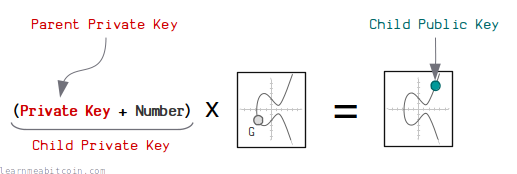
Similarly, if you take that same number and convert it to a point on the curve and add that to the parent public key, you end up with the same child public key:
Code

 copied
copied copied
copiedrequire 'ecdsa' # ECDSA Math (sudo gem install ecdsa)
# Original Private Key and Public Key
private_key = 12345
public_key = ECDSA::Group::Secp256k1.generator.multiply_by_scalar(private_key)
number = rand(1000000) # used to modify the private key and public key independently
# Child Public Key 1: (Private Key + Number) * Generator
private_and_number = private_key + number
child_public_key1 = ECDSA::Group::Secp256k1.generator.multiply_by_scalar(private_and_number)
# Child Public Key 2: Public Key + (Number * Generator)
number_point = ECDSA::Group::Secp256k1.generator.multiply_by_scalar(number)
child_public_key2 = public_key.add_to_point(number_point)
# Results
puts ECDSA::Format::PointOctetString.encode(child_public_key1, compression: true).unpack("H*") #=> e.g. 022861a4809b2d8eb9269abea605f47db91deb9f5385bcc10b94aac6a0b81cba3d
puts ECDSA::Format::PointOctetString.encode(child_public_key2, compression: true).unpack("H*") #=> e.g. 022861a4809b2d8eb9269abea605f47db91deb9f5385bcc10b94aac6a0b81cba3d
puts child_public_key1 == child_public_key2 #=> true
Address
An extended key can be converted to an address to make it easier to pass around.
The address for an extended key contains the private key/public key and chain code, along with some additional metadata.
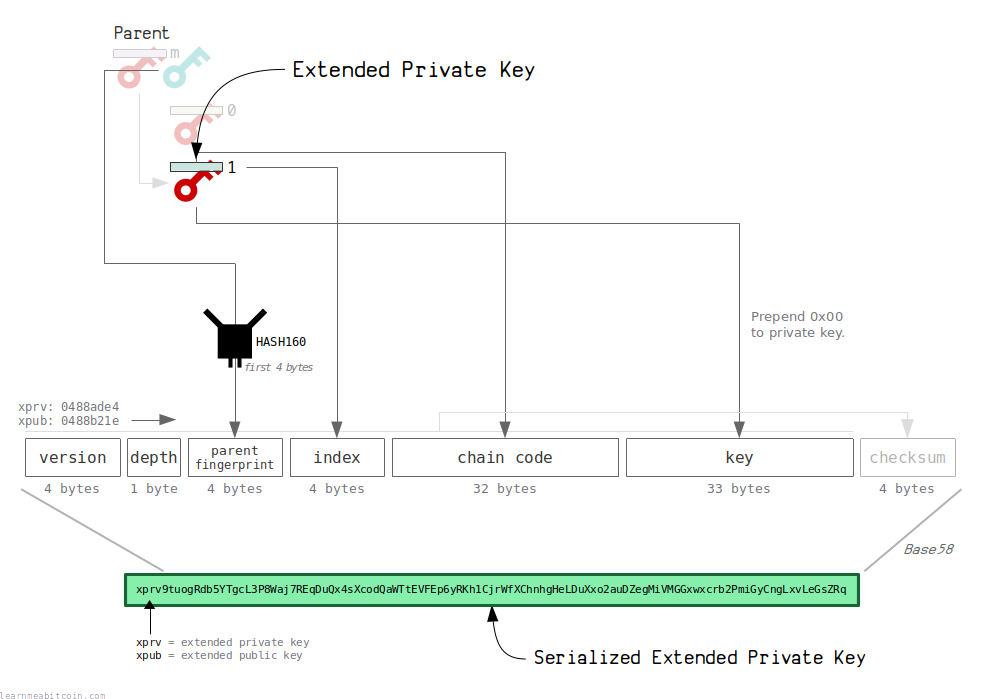
Before converting to an address, an extended key is serialized into the following fields:
| Field | Size (bytes) | Description |
|---|---|---|
| Version | 4 | Places an identifying prefix at the start (e.g. "xprv" = 0488ade4). |
| Depth | 1 | How many derivations deep this extended key is from the master key. |
| Parent Fingerprint | 4 | The first 4 bytes of the HASH160 of the parent's public key. |
| Child Number | 4 | The index number of this child from the parent. |
| Chain Code | 32 | The extra 32 byte secret, preventing others from deriving child keys without it. |
| Key | 33 | The private key (prepended with 00) or public key. |
NotesVersion Bytes: Master Extended Keys: In the Key field, a private key (32 bytes) is prepended with |
||
A checksum is then added to this serialized data (to help detect errors), before finally converting everything to Base58 (to create a human-friendly extended key format).
An extended private key looks like this:
xprv9tuogRdb5YTgcL3P8Waj7REqDuQx4sXcodQaWTtEVFEp6yRKh1CjrWfXChnhgHeLDuXxo2auDZegMiVMGGxwxcrb2PmiGyCngLxvLeGsZRq
An extended public key looks like this:
xpub67uA5wAUuv1ypp7rEY7jUZBZmwFSULFUArLBJrHr3amnymkUEYWzQJz13zLacZv33sSuxKVmerpZeFExapBNt8HpAqtTtWqDQRAgyqSKUHu
As you can see they're pretty long compared to typical addresses, but that's because they contain extra useful information about the extended key.
The fingerprint, depth, and child number are not required for deriving child extended keys – they just help you to identify the current key's parent and position in the tree.
The 4-byte field for the child number is the reason why extended keys are limited to deriving children with indexes between 0 and 4,294,967,295 (0xffffffff).
Code

 copied
copied copied
copied# -----
# Utils - Needed for creating the fingerprint and checksum, and converting hex string to Base58
# -----
require 'digest'
def create_fingerprint(parent_public_key)
hash160 = Digest::RMD160.digest(Digest::SHA256.digest([parent_public_key].pack("H*"))) # hash160 it
fingerprint = hash160[0...4].unpack("H*").join # take first 4 bytes (and convert to hex)
return fingerprint
end
def hash256(hex)
binary = [hex].pack("H*")
hash1 = Digest::SHA256.digest(binary)
hash2 = Digest::SHA256.digest(hash1)
result = hash2.unpack("H*")[0]
return result
end
def checksum(hex)
hash = hash256(hex) # Hash the data through SHA256 twice
return hash[0...8] # Return the first 4 bytes (8 characters)
end
def base58_encode(hex)
chars = %w[
1 2 3 4 5 6 7 8 9
A B C D E F G H J K L M N P Q R S T U V W X Y Z
a b c d e f g h i j k m n o p q r s t u v w x y z
]
base = chars.length
i = hex.to_i(16)
buffer = String.new
while i > 0
remainder = i % base
i = i / base
buffer = chars[remainder] + buffer
end
# add '1's to the start based on number of leading bytes of zeros
leading_zero_bytes = (hex.match(/^([0]+)/) ? $1 : '').size / 2
("1"*leading_zero_bytes) + buffer
end
# --------------------------
# Extended Key Serialization
# --------------------------
parent_public_key = "0252c616d91a2488c1fd1f0f172e98f7d1f6e51f8f389b2f8d632a8b490d5f6da9" # needed to create fingerprint
chain_code = "05aae71d7c080474efaab01fa79e96f4c6cfe243237780b0df4bc36106228e31" # m/0
private_key = "39f329fedba2a68e2a804fcd9aeea4104ace9080212a52ce8b52c1fb89850c72" # m/0
# version + depth + fingerprint + childnumber + chain_code + key + (checksum)
#
# version: puts xprv or xpub at the start
# depth: how many times this child has been derived from master key (0 = master key)
# fingerprint: created from parent public key (allows you to spot adjacent xprv and xpubs)
# childnumber: the index of this child key from the parent
# chain_code: the current chain code being used for this key
# key: the private or public key you want to create a serialized extended key for (prepend 0x00 for private)
version = "0488ade4" # private = 0x0488ade4 (xprv), public = 0x0488b21e (xpub)
depth = "01"
fingerprint = create_fingerprint(parent_public_key) #=> "018c1259"
childnumber = "00000000"
chain_code = chain_code
key = "00" + private_key # prepend 00 to private keys (to make them 33 bytes, the same as public keys)
serialized = version + depth + fingerprint + childnumber + chain_code + key
extended_private_key = base58_encode(serialized + checksum(serialized))
puts "extended_private_key: #{extended_private_key}" #=> xprv9tuogRdb5YTgcL3P8Waj7REqDuQx4sXcodQaWTtEVFEp6yRKh1CjrWfXChnhgHeLDuXxo2auDZegMiVMGGxwxcrb2PmiGyCngLxvLeGsZRq
Code
Here are some complete code examples for creating, deriving, and serializing extended keys in Bitcoin.
Extended Keys (Full Code)

 copied
copied copied
copied<?php
// Note: Requires https://github.com/Bit-Wasp/secp256k1-php
// ------------------
// Seed to Master Key
// ------------------
$seed = "67f93560761e20617de26e0cb84f7234aaf373ed2e66295c3d7397e6d7ebe882ea396d5d293808b0defd7edd2babd4c091ad942e6a9351e6d075a29d4df872af";
echo "seed: $seed".PHP_EOL;
echo PHP_EOL;
// Hash it through HMAC-SHA512 and split in to two halves
//
// seed
// |
// |----|
// |HMAC|
// |----|
// |
// | priv | chain code |
//
$hmac = hash_hmac("sha512", hex2bin($seed), "Bitcoin seed"); // algo, data, key, raw_output (optional)
$master_private_key = substr($hmac, 0, 64); // first half is private key
$master_chain_code = substr($hmac, 64); // second half is chain code
//
// m (priv, chain_code)
//
echo "master_chain_code: $master_chain_code".PHP_EOL;
echo "master_private_key: $master_private_key".PHP_EOL;
// Use elliptic curve mathematics to go from private key to the public key
//
// priv -> pub
//
$context = secp256k1_context_create(SECP256K1_CONTEXT_SIGN | SECP256K1_CONTEXT_VERIFY); // set curve context
$point = null; secp256k1_ec_pubkey_create($context, $point, hex2bin($master_private_key)); // get public key point
$serialized = ''; secp256k1_ec_pubkey_serialize($context, $serialized, $point, SECP256K1_EC_COMPRESSED); // serialize to compressed public key
$master_public_key = bin2hex($serialized);
//
// m (priv, pub, chain_code)
//
echo "master_public_key: $master_public_key".PHP_EOL;
echo PHP_EOL;
// ---------------------------------------------------------
// Parent Extended Private Key to Child Extended Private Key (m/0)
// ---------------------------------------------------------
// m (priv, pub, chain code)
// |
// m/0 (priv, pub, chain code)
$parent_private_key = $master_private_key; // get private key of parent
$parent_chain_code = $master_chain_code; // get chain code of parent
$i = 0; // the index of this child from parent
// Normal Child (extended public key can derive its public keys)
if ($i < 2**31) { // first half of possible indexes are normal children
// Get public key point for the parent private key
$parent_public_key = $master_public_key; // you can derive this from the parent private key using the elliptic curve mathematics above
// The `data` for the upcoming HMAC is the parent public key + index
// data = | parent public key (33 bytes) | i (4 bytes) |
$data = pack("H*", $parent_public_key).pack("N", $i);
}
// Hardened Child (extended public key cannot derive its public keys)
if ($i >= 2**31 ) { // second half of possible indexes are hardened children
// data = | 00 | parent private key (32 bytes) | i (4 bytes) |
$data = pack("H*", "00").pack("H*", $master_private_key).pack("N", $i);
}
// Put data (public key or private key) and chain code through HMAC-SHA512
$hmac = hash_hmac("sha512", $data, hex2bin($parent_chain_code)); // algo, data, key
$left = substr($hmac, 0, 64);
$right = substr($hmac, 64);
// Child chain code is right side of HMAC-SHA512
// m
// |
// m/0 (chain code)
$child_chain_code = $right;
echo "child_chain_code: $child_chain_code".PHP_EOL;
// Check child chain code is valid (not greater than the number of points on the curve)
if (hexdec($child_chain_code) >= 115792089237316195423570985008687907852837564279074904382605163141518161494337) {
throw new Exception("Child chain code is greater than or equal to the order of the elliptic curve. Try next index.");
}
// Calculate child private key (left side of hmac + parent private key) % order
function bchexdec($hex) { // need a utility function to work with addition of large hexadecimal numbers
if(strlen($hex) == 1) {
return hexdec($hex);
} else {
$remain = substr($hex, 0, -1);
$last = substr($hex, -1);
return bcadd(bcmul(16, bchexdec($remain)), hexdec($last));
}
}
function bcdechex($dec) { // need a utility function to convert large integer back to hexadecimal
$last = bcmod($dec, 16);
$remain = bcdiv(bcsub($dec, $last), 16);
if($remain == 0) {
return dechex($last);
} else {
return bcdechex($remain).dechex($last);
}
}
// child private key = (left + parent private key) % order
// m
// |
// m/0 (priv)
$add = bcadd(bchexdec($left), bchexdec($parent_private_key)); // add left side of hmac to parent private key
$mod = bcmod($add, "115792089237316195423570985008687907852837564279074904382605163141518161494337"); // modulus the order of the curve
$child_private_key = str_pad(bcdechex($mod), 64, "0", STR_PAD_LEFT); // ensure it is 64 chars (prepend zeros)
// Check child private key is valid (not zero)
if (hexdec($child_private_key === 0)) {
throw new Exception("Child private key is zero (so it's invalid). Try next index.");
}
echo "child_private_key: $child_private_key".PHP_EOL;
// calculate corresponding child public key from this child private key
// m
// |
// m/0 (pub)
$context = secp256k1_context_create(SECP256K1_CONTEXT_SIGN | SECP256K1_CONTEXT_VERIFY); // set curve context
$point = null; secp256k1_ec_pubkey_create($context, $point, hex2bin($child_private_key)); // get public key point
$serialized = ''; secp256k1_ec_pubkey_serialize($context, $serialized, $point, SECP256K1_EC_COMPRESSED); // serialize to compressed public key
$child_public_key = bin2hex($serialized);
echo "child_public_key: $child_public_key".PHP_EOL; // note may need to pad hex
echo PHP_EOL;
// -------------------------------------------------------
// Parent Extended Public Key to Child Extended Public Key (m/0)
// -------------------------------------------------------
// m -------- p (pub, chain code)
// |
// p/0 (pub, chain code)
$parent_public_key = $master_public_key; // get public key of parent
$parent_chain_code = $master_chain_code; // get chain code of parent
$i = 0; // the index of this child from parent
// Check that you're not trying to create a hardened child public key (extended public keys cannot access public keys of hardened extended private key children)
if ($i >= 2**31) {
throw new Exception("Cannot create a hardened extended child public key. Hardened children of extended private key are private.");
}
// Put data (parent public key + i) and chain code through HMAC-SHA512
$hmac = hash_hmac("sha512", pack("H*", $parent_public_key).pack("N", $i), hex2bin($parent_chain_code)); // same data as when creating normal child extended private key
$left = substr($hmac, 0, 64);
$right = substr($hmac, 64);
// Child chain code is right side of HMAC-SHA512
// m -------- p
// |
// |p/0 (chain code)
$child_chain_code = $right;
echo "child_chain_code: $child_chain_code".PHP_EOL;
// Check child chain code is valid (not greater or equal to than the number of points on the curve)
if (hexdec($child_chain_code) >= 115792089237316195423570985008687907852837564279074904382605163141518161494337) {
throw new Exception("Child chain code is greater than or equal to the order of the elliptic curve. Try next index.");
}
// Calculate child public key: point(parent public key) + hmac left
// m -------- p
// |
// |p/0 (pub)
// point (parent public key)
$context = secp256k1_context_create(SECP256K1_CONTEXT_SIGN | SECP256K1_CONTEXT_VERIFY); // set curve context
$point_public = null; secp256k1_ec_pubkey_parse($context, $point_public, hex2bin($parent_public_key)); // point(parent public key)
// add point(hmac left) to point(parent public key)
secp256k1_ec_pubkey_tweak_add($context, $point_public, hex2bin($left)); // add hmac left to the parent public key point
$add = ''; secp256k1_ec_pubkey_serialize($context, $add, $point_public, SECP256K1_EC_COMPRESSED); // serialize to compressed key
$child_public_key = unpack("H*", $add)[1];
echo "child_public_key: $child_public_key".PHP_EOL;
echo PHP_EOL;
// ----------------------
// Serialize Extended Key
// ----------------------
$parent_public_key = $master_public_key; // needed for creating fingerprint
$chain_code = $child_chain_code;
$private_key = $child_private_key;
// | version | depth | parent fingerprint | index | chain code | key (private or public) |
// | 4 bytes | 1 byte | 4 bytes | 4 bytes | 32 bytes | 33 bytes | = 78 bytes
function create_fingerprint($parent_public_key) {
$hash160 = hash("ripemd160", hash("sha256", hex2bin($parent_public_key), true)); // hash160 the parent public key
return substr($hash160, 0, 8); // return first 4 bytes (8 hex characters)
}
$version = "0488ade4"; // 0488ade4 = private (xprv), 0488b21e = public (xpub)
$depth = "01"; // how many times this child has been derived from master key (0 = master key)
$fingerprint = create_fingerprint($parent_public_key); // fingerprint of parent key - first 4 bytes of hash160(parent public key) (00000000 = master key)
$index = "00000000"; // the index of this child key from the parent (4 byte hexadecimal string)
$chain_code = $chain_code; // chain code for this key
$key = "00".$private_key; // private or public key you want to create a serialized extended key for (prepend 0x00 for private)
// Serialize the data
$serialized = $version.$depth.$fingerprint.$index.$chain_code.$key;
// Create a checksum for it (hash twice through sha256 and take first 4 bytes)
$checksum = substr(hash("sha256", hash("sha256", hex2bin($serialized), true)), 0, 8);
// Base58 encode the serialized+checksum
function base58_encode($hex){
$base58chars = "123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz";
if (strlen($hex) == 0) {
return '';
}
// Convert the hex string to a base10 integer
$num = gmp_strval(gmp_init($hex, 16), 58);
// Check that number isn't just 0 - which would be all padding.
if ($num != '0') {
$num = strtr($num, '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuv', $base58chars);
}
else {
$num = '';
}
// Pad the leading 1's
$pad = '';
$n = 0;
while (substr($hex, $n, 2) == '00') {
$pad .= '1';
$n += 2;
}
return $pad . $num;
}
$master_extended_private_key = base58_encode($serialized.$checksum);
echo "master_extended_private_key: $master_extended_private_key".PHP_EOL;
Resources
- BIP 32 – Original specification for extended keys by Pieter Wuille.
- Ian Coleman BIP39 Tool – Fantastic online tool for deriving extended keys from a seed.
- Bitcoin Ruby: ext_key.rb – Nice implementation of extended keys in Ruby.
- What makes an extended public or private key?
- Why hardened xpub key cannot generate child public key?
- HMAC "Bitcoin Seed" for BIP32
- What is the difference between MAC and HMAC?