Bech32

Address format for segwit locking scripts

Diagram showing the structure of a Bech32 address.

Bech32 ("besh thirty-two") is an address format used for representing segwit locking scripts like P2WPKH, P2WSH, and P2TR.

It was introduced shortly after the Segregated Witness upgrade to provide a better address format for the new segwit locking scripts. It is an improvement over the legacy Base58 format.

Here are some examples of what they look like:

Type Address Length
P2WPKH bc1qx5y8r50l39cap3r9cd65fz7xfvlkjrl258hs8m 42 characters
P2WSH bc1q37qzzxnhnwdsde7yjzq5hc0wktmnqejp3zt0pj9l0pgn9f2gpyls4hahsc 62 characters
P2TR bc1p4pzgu93t5nlw9mscn0v6s7spfya7qntp0afynva267lr0vp0sxyqqj24dc 62 characters

You can identify a Bech32 address by the bc1 prefix.

On this page I'll show you how to encode and decode a Bech32 address, and explain why they're better than Base58 addresses.

Tool

tool-680c0e081ba00
Tool Icon

Bech32

Convert between a ScriptPubKey and a Bech32 address.

0 bytes Type:
ScriptPubKey (bytes)
Version
Witness Program
ScriptPubKey (8-bit groups)
Version
Witness Program
0 bits
ScriptPubKey (5-bit groups)
Version
Witness Program
0 bits
Checksum Constant
Checksum Algorithm
Checksum
Data (Version + Witness Program + Checksum)
Data (Base32)
Bech32
hrp
bc
Network
Separator
1
Data
0 characters
0 secs

Encode

Convert a ScriptPubKey to a Bech32 address

A ScriptPubKey for a segwit locking script (e.g. P2WPKH, P2WSH, P2TR) can be converted to a Bech32 address.

The bulk of the encoding process involves converting the ScriptPubKey bytes into binary (1s and 0s), splitting those 1s and 0s into 5-bit groups, and then converting those 5-bit groups into their corresponding base32 characters.

That's a simplified explanation of the process, but that's basically how it works. The hardest part is calculating the checksum.

Here's a step-by-step guide:

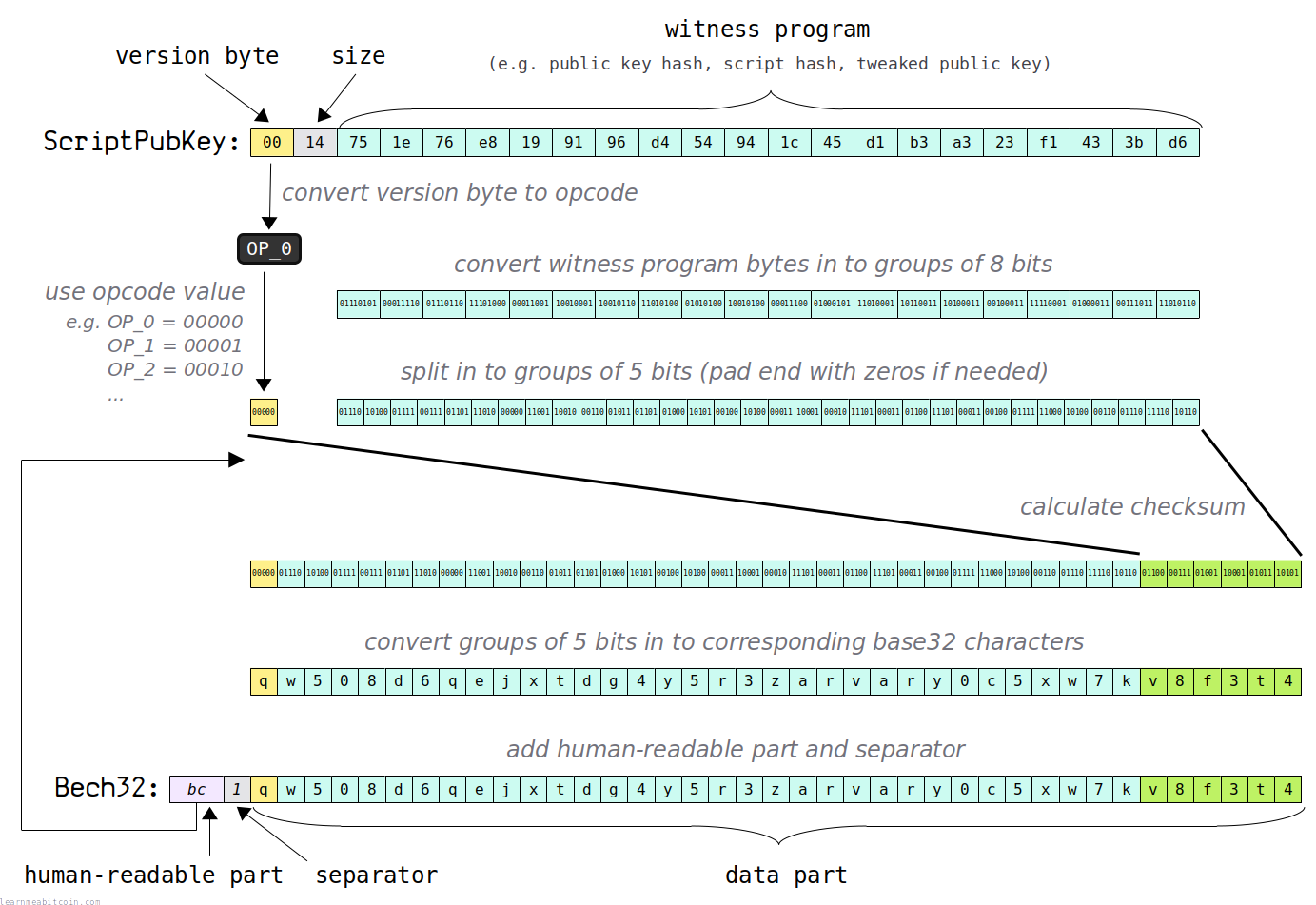
Diagram showing how to encode a segwit ScriptPubKey into a Bech32 address.

The Bech32 encoding is only designed to work for segwit locking scripts (i.e. P2WPKH, P2WSH, P2TR). This is because they follow a specific pattern required for Bech32 encoding (they essentially require a version number and some bytes of data).

1. Human-readable part

To start with, you need to choose what you want the prefix to the final address to be.

In Bitcoin, you have 3 options for this prefix:

This is referred to as the human-readable part, and it indicates whether the address is to be used on mainnet, testnet, or regtest.

You need to choose the human-readable part early on, as this is going to be used to used when calculating the checksum.

2. ScriptPubKey

Next, grab the complete ScriptPubKey that you want to convert to Bech32.

Here's an example P2WPKH ScriptPubKey:

0014751e76e8199196d454941c45d1b3a323f1433bd6

If you're not already aware, each segwit ScriptPubKey follows a similar structure. This structure can be split into 3 parts:

1. Version

The first byte corresponds to an OP_N opcode.

Byte Opcode
00 OP_0
51 OP_1
52 OP_2
53 OP_3
54 OP_4
55 OP_5
56 OP_6
57 OP_7
58 OP_8
59 OP_9
5a OP_10
5b OP_11
5c OP_12
5d OP_13
5e OP_14
5f OP_15
60 OP_16

The integer value that opcode represents indicates the version of the segwit locking script.

In our example, the byte 00 corresponds to the opcode OP_0, which indicates a version 0 segwit locking script (i.e. P2WPKH or P2WSH).

The version byte should be 00, or 51 to 60 (i.e. OP_0 to OP_16).

2. Size

The second byte indicates the size of the upcoming witness program.

This byte is 14 in our example, which indicates that the upcoming witness program is 20 bytes in length.

The size byte is not included as part of the Bech32 encoding. This is because you can figure out the size of the witness program after decoding a Bech32 address, so there's no need to explicitly include the size byte. This saves a character or two in the final address.

3. Witness Program

The remaining data in the ScriptPubKey is the witness program.

This is the unique part of the ScriptPubKey, and usually contains one of 3 types of data:

  1. 20-byte public key hash (P2WPKH)
  2. 32-byte script hash (P2WSH)
  3. 32-byte tweaked public key (P2TR)

In our P2WPKH example, the witness program is a 20-byte public key hash:

751e76e8199196d454941c45d1b3a323f1433bd6

This data has the most influence over what our final Bech32 address looks like.

3. Version (5-bits)

Next, we need to convert the version number of the ScriptPubKey to a 5-bit integer value.

In our example the version byte is 00, which corresponds to the opcode OP_0. Therefore, the version number of this ScriptPubKey is 0. This can then be represented as a 5-bit binary value:

version = 00000

Use the number represented by the opcode, not the byte value. The OP_1 to OP_16 opcodes use the bytes in the range 51 to 60. So it's important to convert the byte to its corresponding OP_N opcode to get the correct version number, rather than using the value of the byte directly.

  • The version number influences the first character after the prefix of the final address.
    • A version 0 segwit locking script starts with bc1q (P2WPKH or P2WSH)
    • A version 1 segwit locking script starts with bc1p (P2TR)
  • The version number must be between 0 and 16, so it will never exceed the maximum 5-bit value (which is 31).

4. Witness Program (8-bit groups)

Next, we convert the witness program into 8-bit groups.

This is what our witness program looks like as a byte array:

witness program = 75 1e 76 e8 19 91 96 d4 54 94 1c 45 d1 b3 a3 23 f1 43 3b d6

If we convert each byte to bits, we get:

witness program = 01110101 00011110 01110110 11101000 00011001 10010001 10010110 11010100 01010100 10010100 00011100 01000101 11010001 10110011 10100011 00100011 11110001 01000011 00111011 11010110

There are 8 bits in a byte.

5. Witness Program (5-bit groups)

Rearrange the witness program from 8-bit groups into 5-bit groups.

witness program = 01110 10100 01111 00111 01101 11010 00000 11001 10010 00110 01011 01101 01000 10101 00100 10100 00011 10001 00010 11101 00011 01100 11101 00011 00100 01111 11000 10100 00110 01110 11110 10110

As you can see, we've rearranged the witness program from 20 x 8-bit groups to 32 x 5-bit groups.

Padding. If you do not have enough bits in the initial 8-bit groups to convert to full 5-bit groups, pad the final 5-bit group with zeros.

6. Checksum

The checksum is calculated using the human-readable part, the 5-bit version, and the 5-bit groups of the witness program.

So this is the data we'll use as the inputs to the checksum algorithm:

hrp             = 'bc'
version         = 00000
witness program = 01110 10100 01111 00111 01101 11010 00000 11001 10010 00110 01011 01101 01000 10101 00100 10100 00011 10001 00010 11101 00011 01100 11101 00011 00100 01111 11000 10100 00110 01110 11110 10110

The resulting checksum for our example is:

checksum = 01100 00111 01001 10001 01011 10101

This process is quite involved, so I've skipped over it for now. See the checksum algorithm for details.

7. Combine

Add the checksum we've just calculated to the end of the 5-bit version and the 5-bit groups of the witness program:

version + witness_program + checksum = 00000 01110 10100 01111 00111 01101 11010 00000 11001 10010 00110 01011 01101 01000 10101 00100 10100 00011 10001 00010 11101 00011 01100 11101 00011 00100 01111 11000 10100 00110 01110 11110 10110 01100 00111 01001 10001 01011 10101

8. Base32

Convert the combined 5-bit groups from the previous step to integers, then use those integers to select the corresponding base32 character for each:

Base32 Characters

0 = q
1 = p
2 = z
3 = r
4 = y
5 = 9
6 = x
7 = 8
8 = g
9 = f
10 = 2
11 = t
12 = v
13 = d
14 = w
15 = 0
16 = s
17 = 3
18 = j
19 = n
20 = 5
21 = 4
22 = k
23 = h
24 = c
25 = e
26 = 6
27 = m
28 = u
29 = a
30 = 7
31 = l

The base32 characters have been arranged in this specific order to improve the error correction capability of the checksum.

For example:

version + witness_program + checksum (5-bit groups) = 00000 01110 10100 01111 00111 01101 11010 00000 11001 10010 00110 01011 01101 01000 10101 00100 10100 00011 10001 00010 11101 00011 01100 11101 00011 00100 01111 11000 10100 00110 01110 11110 10110 01100 00111 01001 10001 01011 10101
version + witness_program + checksum (integers) = 0 14 20 15 7 13 26 0 25 18 6 11 13 8 21 4 20 3 17 2 29 3 12 29 3 4 15 24 20 6 14 30 22 12 7 9 17 11 21
version + witness_program + checksum (base32) = q w 5 0 8 d 6 q e j x t d g 4 y 5 r 3 z a r v a r y 0 c 5 x w 7 k v 8 f 3 t 4

This base32 string forms the data part of the final Bech32 address.

9. Bech32

Finally, add the human-readable part and separator to the start of the base32 string to get the final Bech32 address.

hrp       = bc
separator = 1
base32    = qw508d6qejxtdg4y5r3zarvary0c5xw7kv8f3t4

bech32    = bc1qw508d6qejxtdg4y5r3zarvary0c5xw7kv8f3t4

The separator is always 1. This is used to separate the human-readable part from the base32 data part, because the human-readable part can vary in length. A "1" cannot appear in the data part of the address (as it has been excluded from the base32 character set), which is why it works reliably as a separator character.

Code

 
# --------
# settings
# --------

# human-readable prefix to use in the final Bech32 address
hrp = "bc" # bc = mainnet, tb = testnet

# separator between the human-readable part and the data part
separator = "1" # this is always 1

# base32 character set
characters = "qpzry9x8gf2tvdw0s3jn54khce6mua7l" # all lowercase alphanumeric characters except for "1", "b", "i", "o"

# display full checksum algorithm
display_checksum_algorithm = true # true or false

puts "------------"
puts "scriptpubkey"
puts "------------"
puts

# scriptpubkey we want to convert to Bech32
scriptpubkey = "0014751e76e8199196d454941c45d1b3a323f1433bd6" # example P2WPKH scriptpubkey
puts "scriptpubkey: #{scriptpubkey}"
puts

# split scriptpubkey in to version and witness program
version = scriptpubkey[0..1] # first byte
witness_program = scriptpubkey[4..-1] # bytes 2 to the end
puts "version: #{version}"
puts "program: #{witness_program}"
puts
# note: the size byte between the version and witness program is not used in Bech32 encoding

puts "-------"
puts "version"
puts "-------"
puts

# convert version byte to the integer value represented by its corresponding opcode
#
# 0x00 = OP_0 = 0 (P2WPKH and P2WSH)
# 0x51 = OP_1 = 1 (P2TR)
# 0x52 = OP_2 = 2
# ...
# 0x60 = OP_16 = 16
#
# caution: OP_1 to OP_16 start at 0x51, not 0x01
if (version == "00")
  version_opcode_int = 0
elsif (version.to_i(16) >= 0x51 && version.to_i(16) <= 0x60)
  version_opcode_int = version.to_i(16) - 0x50
else
  puts "Invalid version byte." # the version byte must be between OP_0 and OP_16
  exit
end

# convert version to 5-bit value
version_5_bits = version_opcode_int & 0b11111 # version should already 5 bits (i.e. 0 to 16), but take the last 5 bits just in case

# display version details
puts "version (byte):   #{version}"
puts "version (opcode): OP_#{version_opcode_int}"
puts "version (5-bits): #{version_5_bits.to_s(2).rjust(5, "0")}"
puts

puts "------------"
puts "8-bit groups"
puts "------------"
puts

# convert witness program to 8-bit integer array
version_8_bits = [version_opcode_int] # put 8-bit integer value in to an array
witness_program_8_bits = [witness_program].pack("H*").unpack("C*") # convert hex string to binary, then back in to arrays of 8-bit (1 byte) integers

# display witness program 8-bit array as binary strings
puts "program: #{witness_program_8_bits.map { |v| v.to_s(2).rjust(8, "0") }.join(' ')}"
puts

puts "------------"
puts "5-bit groups"
puts "------------"
puts

# rearrange witness program from 8-bit integer array in to 5-bit integer array
from = 8 # number of bits in starting integer
to   = 5 # number of bits in target integer
accumulator  = 0
counter = 0
max_value = (1 << to) - 1 # max value (5 bits = 0b100000 = 32)
max_accumulator = (1 << (from + to -1)) -1 # 8 bits + 5 bits - 1 bit = 12 bits = 4095 = 0b111111111111
witness_program_5_bits = [] # the return array

# run through each 8-bit integer in the witness program array
witness_program_8_bits.each do |int_8_bits|

  # return nil if negative
  if int_8_bits < 0
    return nil
  end

  # return nil if size of integer is greater than specified size of starting bit group
  if (int_8_bits >> from) != 0
    return nil
  end

  # add starting bits to accumulator
  accumulator = accumulator << from           # << = bitwise left shift
  accumulator = accumulator | int_8_bits      # | = bitwise OR (note: need this comment for code highlighting to work properly on learnmeabitcoin.com website - having a single pipe on one line breaks the syntax highlighting for some reason)
  accumulator = accumulator & max_accumulator # & = bitwise AND

  # increase counter
  counter += from

  # while there are enough bits to produce a new 5-bit group
  while counter >= to

    # decrease counter
    counter -= to

    # add 5-bit value to result
    witness_program_5_bits << ((accumulator >> counter) & max_value)
  end
end

# add padding
if (counter > 0)
  witness_program_5_bits << ((accumulator << (to - counter)) & max_value)
end

# display result
puts "program: #{witness_program_5_bits.map { |v| v.to_s(2).rjust(5, "0") }.join(' ')}"
puts

puts "------------------"
puts "checksum algorithm"
puts "------------------"
puts

# display human-readable part
puts "hrp:          #{hrp}"

# convert human-readable to corresponding UTF-8 character values
hrp_values = hrp.split("").map { |c| c.ord }
puts "hrp_values:   #{hrp_values.map { |v| v.to_s(2).rjust(8, "0") }.join(' ')}"

# expand human-readable part in to 5-bit groups
hrp_expanded = []

# take the first 3 bits of each character's integer value
hrp_values.each do |v|
  hrp_expanded << (v >> 5) # shift 5 bits to the right to get first 3 bits
end

# add separator
hrp_expanded << 0

# take the last 5 bits of each character's integer value
hrp_values.each do |v|
  hrp_expanded << (v & 0b11111) # use bitmask to extract last 5 bits
end

# display result
puts "hrp_expanded: #{hrp_expanded.map { |v| v.to_s(2).rjust(5, "0") }.join(' ')}"
puts

# combine the expanded human-readable part with the version and witness program (all 5-bit groups)
combined = hrp_expanded + [version_5_bits] + witness_program_5_bits

# add padding
combined_with_padding = combined + [0, 0, 0, 0, 0, 0]
puts "hrp + version + program + padding: #{combined_with_padding.map { |v| v.to_s(2).rjust(5, "0") }.join(' ')}"
puts

# checksum generator values
generator = [
  0b111011011010100101011110110010, # 0x3b6a57b2
  0b100110010100001000111001101101, # 0x26508e6d
  0b011110101000010001100111111010, # 0x1ea119fa
  0b111101010000100011001111011101, # 0x3d4233dd
  0b101010000101000110001010110011, # 0x2a1462b3
]

# initial checksum value (final checksum result will be 30 bits)
checksum = 1

# run through each 5-bit group in the combined array
combined_with_padding.each do |v|

  # display current checksum value
  puts "checksum: #{checksum.to_s(2).rjust(30, "0")}" if display_checksum_algorithm
  
  # remove 25 bits from the right of the current checksum value and store the result
  top = checksum >> 25
  puts "top:      #{top.to_s(2).rjust(5, "0")}" if display_checksum_algorithm

  # extract the bottom 25 bits from the current checksum value using a bitmask
  checksum = checksum & 0b1111111111111111111111111
  puts "bottom:        #{checksum.to_s(2).rjust(25, "0")}" if display_checksum_algorithm

  # left shift the checksum value (add 5 zero bits to the end, which creates space for xor'ing with the current 5-bit current value)
  checksum = checksum << 5
  puts "padded:        #{checksum.to_s(2).rjust(30, "0")}" if display_checksum_algorithm

  # xor the current checksum with the next 5-bit value
  checksum = checksum ^ v
  puts "5-bit group:                            #{v.to_s(2).rjust(5, "0")}" if display_checksum_algorithm
  puts "xor:           #{checksum.to_s(2).rjust(30, "0")}" if display_checksum_algorithm

  # run through the last 5 bits of the top value
  5.times do |i|

    # show current generator
    print "generator #{i}:   #{generator[i].to_s(2).rjust(30, "0")}" if display_checksum_algorithm

    # if the next bit of the top value is 1
    if ((top >> i) & 1) == 1

      # xor the current checksum with the corresponding generator value
      checksum = checksum ^ generator[i]

      # add indicator if this generator value was used for xor'ing
      puts " xor" if display_checksum_algorithm
    else 
      puts if display_checksum_algorithm
    end
  end

  # display checksum value after this 5-bit group
  puts "checksum:      #{checksum.to_s(2).rjust(30, "0")}" if display_checksum_algorithm
  puts if display_checksum_algorithm

end

# display checksum value after running through all 5-bit groups
puts "checksum:      #{checksum.to_s(2).rjust(30, "0")}" if display_checksum_algorithm

# set the constant to xor the checksum with based on the version number
if (version_opcode_int == 0)
  constant = 1 # bech32
else
  constant = 0x2bc830a3 # bech32m
end

# display constant
puts "constant:      #{constant.to_s(2).rjust(30, "0")}" if display_checksum_algorithm

# xor the checksum with the constant
checksum = checksum ^ constant

# display constant and final checksum value
puts "checksum:      #{checksum.to_s(2).rjust(30, "0")}" if display_checksum_algorithm
puts if display_checksum_algorithm

# convert the checksum in to 6 groups of 5-bits
checksum_5_bits = []

# we want 6 groups of 5 bits
6.times do |i|

  # calculate the right shift amount so we can grab each 5-bit group from the 30-bit checksum
  right_shift = 5 * (5 - i)

  # shift the checksum value to the right
  shifted = (checksum >> right_shift)

  # extract the last 5 bits from the shifted value
  bits = shifted & 0b11111

  # add the 5-bit group to the checksum array
  checksum_5_bits << bits
end

# display result
puts "checksum: #{checksum_5_bits.map { |v| v.to_s(2).rjust(5, "0") }.join(' ')}"
puts

puts "------"
puts "base32"
puts "------"
puts

# combine the version, program, and checksum
data = [version_5_bits] + witness_program_5_bits + checksum_5_bits
puts "version + program + checksum: #{data.map { |v| v.to_s(2).rjust(5, "0") }.join(' ')}"
puts "version + program + checksum: #{data.map { |v| v }.join(' ')}"

# convert each 5-bit group to its corresponding base32 character
base32 = data.map { |i| characters[i] }
puts "base32: #{base32.join(' ')}"
puts

puts "------"
puts "bech32"
puts "------"
puts

# display the hrp and separator
puts "hrp:       #{hrp}"
puts "separator: #{separator}"
puts

# combine the human-readable part, separator, and base32 data
bech32 = hrp + separator + base32.join
puts "bech32:    #{bech32}" # bc1qw508d6qejxtdg4y5r3zarvary0c5xw7kv8f3t4

Decode

Convert a Bech32 address to a ScriptPubKey

A Bech32 address can be decoded into a segwit ScriptPubKey.

To do this, you basically convert the base32 characters into their corresponding 5-bit values, rearrange those bits into 8-bit groups to get the hex byte values, and then reconstruct the complete ScriptPubKey.

Here's a step-by-step guide:

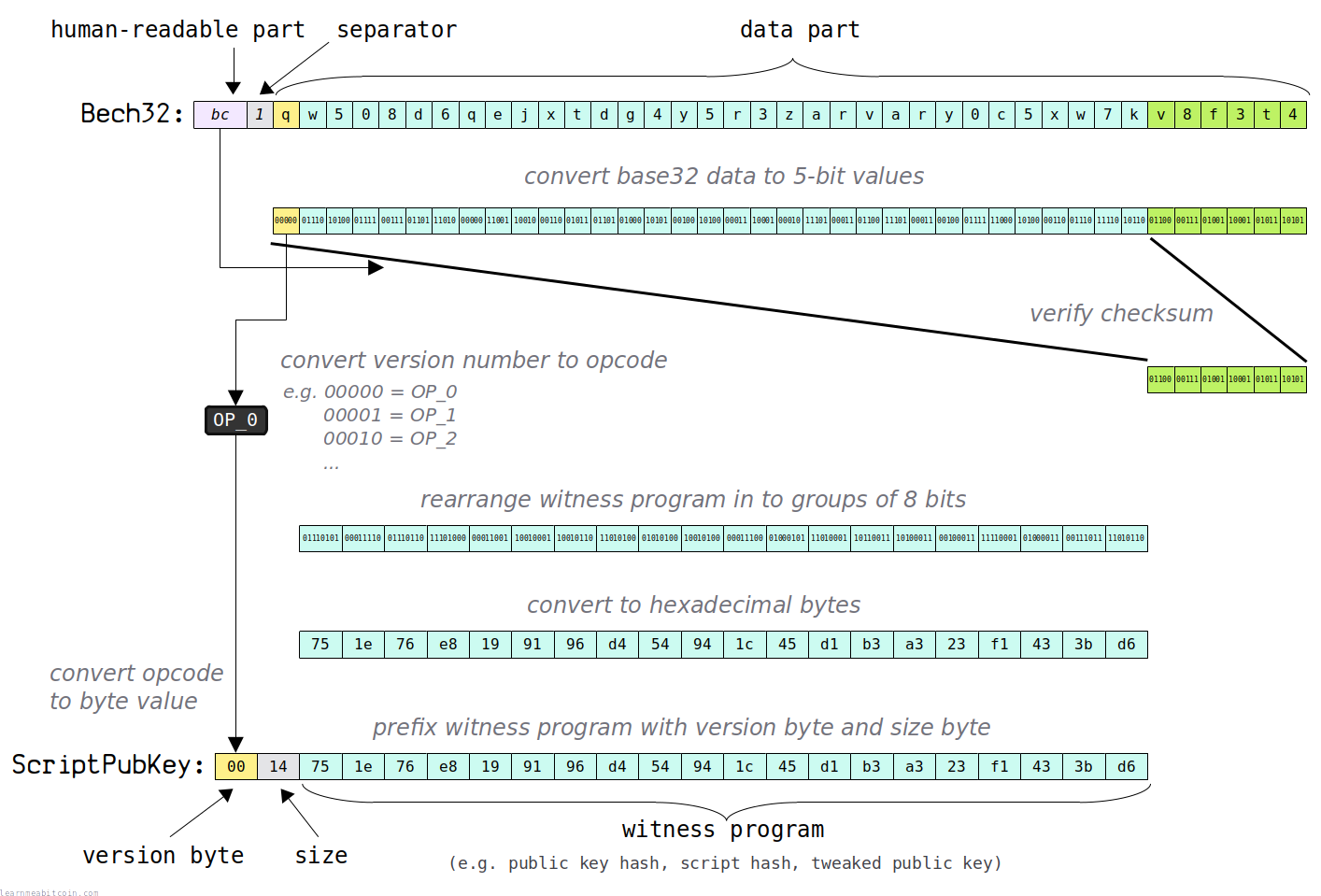
Diagram showing how to decode a Bech32 address to a segwit ScriptPubKey.

1. Address

First of all, grab the address you want to convert to a ScriptPubKey.

Here's an example:

bc1qw508d6qejxtdg4y5r3zarvary0c5xw7kv8f3t4

Next, you need to split the address into 3 parts:

  1. Human-readable part. The characters before the separator are the human-readable part. This part can be between 1 and 83 characters in length. In Bitcoin, this part indicates whether the address is used on mainnet ("bc"), testnet ("tb"), or regest ("bcrt").
  2. Separator. The last occurrence of a "1" in the address is the separator. This separates the human-readable part from the data part. A valid address must contain a "1" separator character.
  3. Data. Everything after the separator is the "data" part. This is a base32 encoding of the version, witness program, and checksum.

The way to split a Bech32 address into the human-readable part and the data part is by looking for the separator, which is the last occurrence of a "1" character.

So for this address, we have:

  1. Human-readable part = bc
  2. Separator = 1
  3. Data = qw508d6qejxtdg4y5r3zarvary0c5xw7kv8f3t4
  • Do not read a fixed number of characters to extract the human-readable part. It's usually 2 or 4 characters, but it can technically be between 1 and 83 characters in length in future.
  • Do not search for the first occurrence of a "1". It's technically possible for the human-readable part to contain a "1", so you would end up splitting the address too early and have an incorrect data part. To be sure you're getting the correct position of the separator, you should scan for the last occurrence of a "1" instead.

The separator is not used from here on out. Moving forward we will only use the human-readable part and the data part.

2. 5-bit groups

Convert the data part from base32 characters into their corresponding 5-bit integer values.

For example:

base32 = qw508d6qejxtdg4y5r3zarvary0c5xw7kv8f3t4
integers = 0 14 20 15 7 13 26 0 25 18 6 11 13 8 21 4 20 3 17 2 29 3 12 29 3 4 15 24 20 6 14 30 22 12 7 9 17 11 21

Base32 Characters

0 = q
1 = p
2 = z
3 = r
4 = y
5 = 9
6 = x
7 = 8
8 = g
9 = f
10 = 2
11 = t
12 = v
13 = d
14 = w
15 = 0
16 = s
17 = 3
18 = j
19 = n
20 = 5
21 = 4
22 = k
23 = h
24 = c
25 = e
26 = 6
27 = m
28 = u
29 = a
30 = 7
31 = l

This array of integers can be split into 3 parts:

  1. Version. The first integer represents the version.
  2. Witness Program. The integers between the version and checksum are the witness program.
  3. Checksum. The last 6 integers are the checksum.

So we have:

version         = 0
witness program = 14 20 15 7 13 26 0 25 18 6 11 13 8 21 4 20 3 17 2 29 3 12 29 3 4 15 24 20 6 14 30 22
checksum        = 12 7 9 17 11 21

If you like, you can display these integers in their 5-bit binary representations:

version         = 00000
witness program = 01110 10100 01111 00111 01101 11010 00000 11001 10010 00110 01011 01101 01000 10101 00100 10100 00011 10001 00010 11101 00011 01100 11101 00011 00100 01111 11000 10100 00110 01110 11110 10110
checksum        = 01100 00111 01001 10001 01011 10101

I'm displaying the 5-bit integers in binary for visual purposes. You don't need to do this when decoding, as it's fine to keep them as arrays of 5-bit integers.

3. Verify checksum

Next we should verify that the checksum in the address is valid.

To do this, we calculate the checksum using the human-readable part from step 1, and the version and witness program we've decoded from step 2:

checksum (calculated) = 01100 00111 01001 10001 01011 10101

We then compare this to the checksum provided in the address:

checksum (address)    = 01100 00111 01001 10001 01011 10101

If the checksums match, we know that the address has been entered correctly and no mistakes have been made.

This is just a simple check. The checksum actually allows you to detect the position of potential errors and provide suggestions on how to correct them.

4. Version

Next, the version integer needs to be converted to a hex byte corresponding to a OP_N opcode.

For example:

Version Opcode Hex
0 OP_0 00
1 OP_1 51
2 OP_2 52
... ... ...
16 OP_16 60

The version is 0 in our example, which corresponds to the OP_0 opcode, which is represented by the following hex byte:

version = 00

Quick conversion. If the version is greater than zero, add 0x51 to get the OP_N opcode byte value.

  • Do not convert the version integer value directly to a hex byte. For example, version 1 corresponds to OP_1, which is represented by the byte 51. If you convert it directly to hex you'll get 01, which is an invalid opcode for the version number.
  • The version number must be between 0 and 16. Any other version number is invalid.

5. 8-bit groups

Rearrange the witness program from 5-bit groups into 8-bit groups:

witness program (5-bit groups) = 01110 10100 01111 00111 01101 11010 00000 11001 10010 00110 01011 01101 01000 10101 00100 10100 00011 10001 00010 11101 00011 01100 11101 00011 00100 01111 11000 10100 00110 01110 11110 10110

witness program (8-bit groups) = 01110101 00011110 01110110 11101000 00011001 10010001 10010110 11010100 01010100 10010100 00011100 01000101 11010001 10110011 10100011 00100011 11110001 01000011 00111011 11010110

As you can see, we've simply gathered the bits into 8-bit groups.

Check that the 5-bit groups do not contain too much padding. If the remainder after dividing the total number of bits in the 5 bit groups by the total number of bits in the resulting 8 bit groups is 5 or greater, then the address contained too much padding.

Check that the padding contains zeros only. The padding amount is the total number of bits in the 5-bit groups minus the total number of bits in the 8-bit groups. If this padding contains anything other than zeros, the padding is invalid.

If we convert these 8-bit groups into hex bytes we get:

witness program (bytes) = 75 1e 76 e8 19 91 96 d4 54 94 1c 45 d1 b3 a3 23 f1 43 3b d6

6. ScriptPubKey

Finally, to construct the final ScriptPubKey we first need to calculate the size of the witness program from the previous step.

In our example, the witness program is 20 bytes in length, which as a hex byte is 14. This gives us:

version = 00
size = 14
witness program = 75 1e 76 e8 19 91 96 d4 54 94 1c 45 d1 b3 a3 23 f1 43 3b d6

If we combine these 3 pieces of data, we have our complete ScriptPubKey:

scriptpubkey = 0014751e76e8199196d454941c45d1b3a323f1433bd6

Seeing as this is version 0 with a 20-byte witness program, we can tell this is a P2WPKH locking script.

Code

 
# --------
# settings
# --------

# base32 character set
characters = "qpzry9x8gf2tvdw0s3jn54khce6mua7l" # all lowercase alphanumeric characters except for "1", "b", "i", "o"

# display full checksum algorithm
display_checksum_algorithm = false # true or false

puts "-------"
puts "address"
puts "-------"
puts

# Bech32 address we want to convert to a scriptpubkey
address = "bc1qw508d6qejxtdg4y5r3zarvary0c5xw7kv8f3t4" # example P2WPKH scriptpubkey
puts "address:   #{address}"
puts

# find the position of the separator (the last occurrence of a "1")
separator_position = address.rindex("1")
# note: the separator is always "1"
# caution: you want the _last_ occurrence of "1" as the human-readable part could potentially contain "1"

# everything before the separator is the human-readable part
hrp = address[0..separator_position - 1]

# everything after the separator is the data part
data = address[separator_position + 1..-1]

puts "hrp:       #{hrp}"
puts "data:      #{data}"
puts
# note: the separator is not used when converting the address to a scriptpubkey

puts "------------"
puts "5-bit groups"
puts "------------"
puts

# convert each base32 character to its corresponding 5-bit integer value
data_5_bits = data.split("").map { |c| characters.index(c) }

# first 5-bit group is the version
version_5_bits = data_5_bits.shift

# last 6 5-bit groups are the checksum
checksum_5_bits = data_5_bits.pop(6)

# remaining 5-bit groups are the witness program
witness_program_5_bits = data_5_bits

# display the 5-bit groups as integers
puts "version:   #{version_5_bits}"
puts "program:   #{witness_program_5_bits.join(' ')}"
puts "checksum:  #{checksum_5_bits.join(' ')}"
puts

# show the 5-bit groups as binary strings
puts "version:   #{version_5_bits.to_s(2).rjust(5, "0")}"
puts "program:   #{witness_program_5_bits.map { |v| v.to_s(2).rjust(5, "0") }.join(' ')}"
puts "checksum:  #{checksum_5_bits.map { |v| v.to_s(2).rjust(5, "0") }.join(' ')}"
puts

puts "---------------------"
puts "checksum verification"
puts "---------------------"
puts
# calculate the checksum from the given hrp and witness program

# convert human-readable to corresponding UTF-8 character values
hrp_values = hrp.split("").map { |c| c.ord }

# expand human-readable part in to 5-bit groups
hrp_expanded = []

# take the first 3 bits of each character's integer value
hrp_values.each do |v|
  hrp_expanded << (v >> 5) # shift 5 bits to the right to get first 3 bits
end

# add separator
hrp_expanded << 0

# take the last 5 bits of each character's integer value
hrp_values.each do |v|
  hrp_expanded << (v & 0b11111) # use bitmask to extract last 5 bits
end

# combine the expanded human-readable part with the version and witness program (all 5-bit groups)
combined = hrp_expanded + [version_5_bits] + witness_program_5_bits

# add padding
combined_with_padding = combined + [0, 0, 0, 0, 0, 0]

# checksum generator values
generator = [
  0b111011011010100101011110110010, # 0x3b6a57b2
  0b100110010100001000111001101101, # 0x26508e6d
  0b011110101000010001100111111010, # 0x1ea119fa
  0b111101010000100011001111011101, # 0x3d4233dd
  0b101010000101000110001010110011, # 0x2a1462b3
]

# initial checksum value (final checksum result will be 30 bits)
checksum = 1

# run through each 5-bit group in the combined array
combined_with_padding.each do |v|
  
  # remove 25 bits from the right of the current checksum value and store the result
  top = checksum >> 25

  # extract the lower 25 bits from the current checksum value using a bitmask
  checksum = checksum & 0b1111111111111111111111111

  # left shift the checksum value (add 5 zero bits to the end, which creates space for xor'ing with the current 5-bit current value)
  checksum = checksum << 5

  # xor the current checksum with the next 5-bit value
  checksum = checksum ^ v

  # run through the last 5 bits of the top value
  5.times do |i|

    # if the next bit of the top value is 1
    if ((top >> i) & 1) == 1

      # xor the current checksum with the corresponding generator value
      checksum = checksum ^ generator[i]
    end
  end

end

# set the constant to xor the checksum with based on the version number
if (version_5_bits == 0)
  constant = 1 # bech32
else
  constant = 0x2bc830a3 # bech32m
end

# display constant
puts "constant:      #{constant.to_s(2).rjust(30, "0")}" if display_checksum_algorithm

# xor the checksum with the constant
checksum = checksum ^ constant

# convert the checksum in to 6 groups of 5-bits
checksum_verify = []

# we want 6 groups of 5 bits
6.times do |i|

  # calculate the right shift amount so we can grab each 5-bit group from the 30-bit checksum
  right_shift = 5 * (5 - i)

  # shift the checksum value to the right
  shifted = (checksum >> right_shift)

  # extract the last 5 bits from the shifted value
  bits = shifted & 0b11111

  # add the 5-bit group to the checksum array
  checksum_verify << bits
end

# display calculated checksum
print "checksum:  #{checksum_verify.map { |v| v.to_s(2).rjust(5, "0") }.join(' ')}"

# check the calculated checksum matches the checksum in the address
if checksum_5_bits == checksum_verify
  puts " ✓"
else
  puts " ✗"
end
puts


puts "-------"
puts "version"
puts "-------"
puts

# convert version integer value to its corresponding OP_N hex byte
if (version_5_bits == 0)
  version_op_n_hex = version_5_bits.to_s(16).rjust(2, "0") # OP_0
else
  version_op_n_hex = (version_5_bits + 0x50).to_s(16).rjust(2, "0") # OP_1 to OP_16
end

puts "5-bits:    #{version_5_bits.to_s(2).rjust(5, "0")}"
puts "opcode:    OP_#{version_5_bits}"
puts "hex:       #{version_op_n_hex}"
puts


puts "------------"
puts "8-bit groups"
puts "------------"
puts

# rearrange witness program from 5-bit integer array in to 8-bit integer array
from = 5 # number of bits in starting integer
to   = 8 # number of bits in target integer
accumulator  = 0
counter = 0
max_value = (1 << to) - 1 # max value (5 bits = 0b100000 = 32)
max_accumulator = (1 << (from + to -1)) -1 # 8 bits + 5 bits - 1 bit = 12 bits = 4095 = 0b111111111111
witness_program_8_bits = [] # the return array

# run through each 5-bit integer in the witness program array
witness_program_5_bits.each do |int_5_bits|

  # return nil if negative
  if int_5_bits < 0
    return nil
  end

  # return nil if size of integer is greater than specified size of starting bit group
  if (int_5_bits >> from) != 0
    return nil
  end

  # add starting bits to accumulator
  accumulator = accumulator << from           # << = bitwise left shift
  accumulator = accumulator | int_8_bits      # | = bitwise OR (note: need this comment for code highlighting to work properly on learnmeabitcoin.com website - having a single pipe on one line breaks the syntax highlighting for some reason)
  accumulator = accumulator & max_accumulator # & = bitwise AND

  # increase counter
  counter += from

  # while there are enough bits to produce a new 8-bit group
  while counter >= to

    # decrease counter
    counter -= to

    # add 8-bit value to result
    witness_program_8_bits << ((accumulator >> counter) & max_value)
  end
end

# display result
puts "program:   #{witness_program_8_bits.map { |v| v.to_s(2).rjust(8, "0") }.join(' ')}"
puts

puts "------------"
puts "scriptpubkey"
puts "------------"
puts

# calculate the size of the witness program and convert to hex byte
witness_program_size_hex = witness_program_8_bits.size.to_s(16).rjust(2, "0")

# convert witness program to hex
witness_program_hex = witness_program_8_bits.map { |v| v.to_s(16).rjust(2, "0") }.join

# display the version, size, and witness program as hex
puts "version:   #{version_op_n_hex}"
puts "size:      #{witness_program_size_hex}"
puts "program:   #{witness_program_hex}"
puts

# combine the version, size, and witness program in to a scriptpubkey
scriptpubkey = version_op_n_hex + witness_program_size_hex + witness_program_hex
puts "scriptpubkey: #{scriptpubkey}" # 0014751e76e8199196d454941c45d1b3a323f1433bd6

Checksum

How do you calculate a Bech32 checksum?

The most complex part of the Bech32 encoding is calculating the checksum.

The checksum algorithm uses BCH codes, which allows for error correction across the data (which is not possible with the simple checksum used in Base58). This makes the Bech32 checksum a lot more useful, but also more complex to calculate.

I don't know enough about BCH codes to explain the design of the algorithm, so I'll just show you how to calculate the checksum instead.

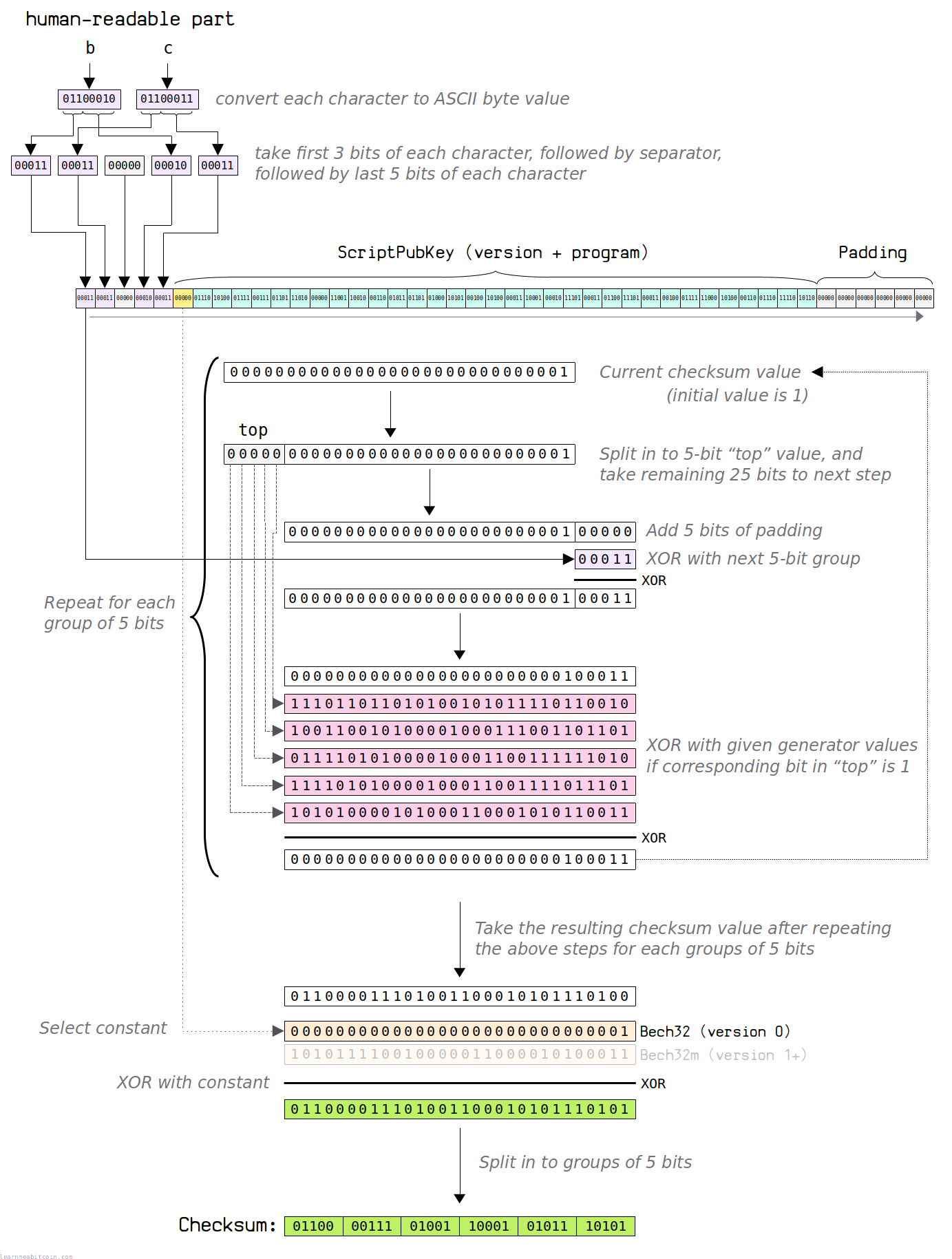
Diagram showing how to calculate the checksum for a Bech32 address.

1. Prepare data

The checksum for a Bech32 address is calculated from the following data:

  1. Human-readable part. The prefix you want to use for the final address needs to be selected before creating the checksum. This string is usually 'bc' (mainnet), 'tb' (testnet), or 'bcrt' (testnet).
  2. Version. This is the version number for the segwit ScriptPubKey. This is a 5-bit integer value indicated by an OP_N opcode.
  3. Witness Program. This is the witness program from the ScriptPubKey as an array of 5-bit values. So if you're calculating the checksum from a raw ScriptPubKey, you need to rearrange the witness program from an array of 8-bit bytes to an array of 5-bit values first.

Here's some example data:

hrp             = 'bc'
version         = 00000
witness program = 01110 10100 01111 00111 01101 11010 00000 11001 10010 00110 01011 01101 01000 10101 00100 10100 00011 10001 00010 11101 00011 01100 11101 00011 00100 01111 11000 10100 00110 01110 11110 10110

The size byte from the ScriptPubKey and the separator in the address are not covered by the checksum.

2. Expand human-readable part

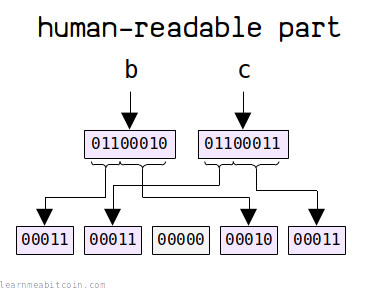
 Diagram showing how to expand the human-readable part into 5-bit groups.

The human-readable part is used as the prefix for the address. This needs to be included as part of the checksum so that we can detect if it has been entered correctly.

This prefix is a string of 1 to 83 US-ASCII characters. Therefore, we need to "expand" these characters to turn them into an array of 5-bit values.

This is how you expand the human-readable part:

  1. Convert each character to its 8-bit ASCII byte value.
  2. Take the first 3 bits of each character's byte value.
  3. Add a zero as a separator.
  4. Take the last 5 bits of each character's byte value.

So basically, seeing as each ASCII character represents an 8-bit value, we split them up so that we can get an array of 5-bit values instead.

For example:

hrp            = 'bc'
hrp (ASCII)    = 01100010 01100011
hrp (expanded) = 00011 00011 00000 00010 00011

The human-readable part is now represented as a 5-bit integer array. This matches the structure of the version and witness program (which are also in arrays of 5-bit integers).

3. Construct 5-bit array

The input to the checksum algorithm is a 5-bit array of the following data:

  1. Expanded human-readable part. The 5-bit integer array from step 2.
  2. Version. A 5-bit integer based on the OP_N opcode value.
  3. Witness program. An array of 5-bit integers.
  4. Padding. An array of 6 zero 5-bit integers.

So you basically take the hrp, version, and witness program, and add some padding to the end.

For example:

hrp (expanded)  = 00011 00011 00000 00010 00011
version         = 00000
witness program = 01110 10100 01111 00111 01101 11010 00000 11001 10010 00110 01011 01101 01000 10101 00100 10100 00011 10001 00010 11101 00011 01100 11101 00011 00100 01111 11000 10100 00110 01110 11110 10110
padding         = 00000 00000 00000 00000 00000 00000

5-bit array     = 00011 00011 00000 00010 00011 00000 01110 10100 01111 00111 01101 11010 00000 11001 10010 00110 01011 01101 01000 10101 00100 10100 00011 10001 00010 11101 00011 01100 11101 00011 00100 01111 11000 10100 00110 01110 11110 10110 00000 00000 00000 00000 00000 00000

This combined array of 5-bit integers is the input to the main checksum algorithm.

4. Generators

This is the fun part.

The final checksum is going to be a 30-bit value. The starting value for the checksum is 1, so our initial checksum looks like this:

000000000000000000000000000001

We will now run through each 5-bit integer in our array, and perform the following steps:

1. Top

Grab the first 5 bits of the current checksum value. This is the "top" value, and will be used in a later step.

top = 00000

2. Bottom

Grab the lower 25 bits of the current checksum value. This is the "bottom" value, and this is what we are going to adjust.

bottom = 0000000000000000000000001

3. Padding

Add 5 bits of padding to the "bottom" 25 bits from the previous step to make 30 bits in total.

padded = 000000000000000000000000100000

4. XOR with next 5-bit value

Take the next 5-bit value from the array and XOR it with the padded 30-bit checksum value from the previous step:

padded      = 000000000000000000000000100000
5-bit value =                          00011
xor         = 000000000000000000000000100011

5. XOR with generator values

We now XOR the value from the previous step with the following generator values:

generator 0 = 111011011010100101011110110010
generator 1 = 100110010100001000111001101101
generator 2 = 011110101000010001100111111010
generator 3 = 111101010000100011001111011101
generator 4 = 101010000101000110001010110011

However, we do not always XOR with all of these generator values. Instead, we use the "top" value to determine which generator values we actually XOR with.

Using the "top" value, we read the bits from right-to-left to determine which generator values we XOR the current checksum value with. If the bit is set (i.e. "1"), XOR with that corresponding generator value.

Using our current example:

top = 00000

generator 0 = 111011011010100101011110110010 (bit 4 = 0, do not XOR)
generator 1 = 100110010100001000111001101101 (bit 3 = 0, do not XOR)
generator 2 = 011110101000010001100111111010 (bit 2 = 0, do not XOR)
generator 3 = 111101010000100011001111011101 (bit 1 = 0, do not XOR)
generator 4 = 101010000101000110001010110011 (bit 0 = 0, do not XOR)
xor         = 000000000000000000000000100011

result      = 000000000000000000000000100011

None of the bits in "top" are set, so we do not XOR the current checksum value with any of the generators.

If the right-most bit is set, we XOR with generator 0. If the next bit from the right is set, we also XOR with generator 1, and so on.

6. Repeat

Repeat the previous steps for all 5-bit integers in the array.

Full step-by-step calculations
 
checksum: 000000000000000000000000000001
top:      00000
bottom:        0000000000000000000000001
padded:        000000000000000000000000100000
5-bit group:                            00011
xor:           000000000000000000000000100011
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      000000000000000000000000100011

checksum: 000000000000000000000000100011
top:      00000
bottom:        0000000000000000000100011
padded:        000000000000000000010001100000
5-bit group:                            00011
xor:           000000000000000000010001100011
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      000000000000000000010001100011

checksum: 000000000000000000010001100011
top:      00000
bottom:        0000000000000010001100011
padded:        000000000000001000110001100000
5-bit group:                            00000
xor:           000000000000001000110001100000
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      000000000000001000110001100000

checksum: 000000000000001000110001100000
top:      00000
bottom:        0000000001000110001100000
padded:        000000000100011000110000000000
5-bit group:                            00010
xor:           000000000100011000110000000010
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      000000000100011000110000000010

checksum: 000000000100011000110000000010
top:      00000
bottom:        0000100011000110000000010
padded:        000010001100011000000001000000
5-bit group:                            00011
xor:           000010001100011000000001000011
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      000010001100011000000001000011

checksum: 000010001100011000000001000011
top:      00001
bottom:        0001100011000000001000011
padded:        000110001100000000100001100000
5-bit group:                            00000
xor:           000110001100000000100001100000
generator 0:   111011011010100101011110110010 xor
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      111101010110100101111111010010

checksum: 111101010110100101111111010010
top:      11110
bottom:        1010110100101111111010010
padded:        101011010010111111101001000000
5-bit group:                            01110
xor:           101011010010111111101001001110
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101 xor
generator 4:   101010000101000110001010110011 xor
checksum:      000100111011000011110010110111

checksum: 000100111011000011110010110111
top:      00010
bottom:        0111011000011110010110111
padded:        011101100001111001011011100000
5-bit group:                            10100
xor:           011101100001111001011011110100
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      111011110101110001100010011001

checksum: 111011110101110001100010011001
top:      11101
bottom:        1110101110001100010011001
padded:        111010111000110001001100100000
5-bit group:                            01111
xor:           111010111000110001001100101111
generator 0:   111011011010100101011110110010 xor
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101 xor
generator 4:   101010000101000110001010110011 xor
checksum:      001000011111100000110000001001

checksum: 001000011111100000110000001001
top:      00100
bottom:        0011111100000110000001001
padded:        001111110000011000000100100000
5-bit group:                            00111
xor:           001111110000011000000100100111
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      010001011000001001100011011101

checksum: 010001011000001001100011011101
top:      01000
bottom:        1011000001001100011011101
padded:        101100000100110001101110100000
5-bit group:                            01101
xor:           101100000100110001101110101101
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101 xor
generator 4:   101010000101000110001010110011
checksum:      010001010100010010100001110000

checksum: 010001010100010010100001110000
top:      01000
bottom:        1010100010010100001110000
padded:        101010001001010000111000000000
5-bit group:                            11010
xor:           101010001001010000111000011010
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101 xor
generator 4:   101010000101000110001010110011
checksum:      010111011001110011110111000111

checksum: 010111011001110011110111000111
top:      01011
bottom:        1011001110011110111000111
padded:        101100111001111011100011100000
5-bit group:                            00000
xor:           101100111001111011100011100000
generator 0:   111011011010100101011110110010 xor
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101 xor
generator 4:   101010000101000110001010110011
checksum:      001100100111110101001011100010

checksum: 001100100111110101001011100010
top:      00110
bottom:        0100111110101001011100010
padded:        010011111010100101110001000000
5-bit group:                            11001
xor:           010011111010100101110001011001
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      101011000110111100101111001110

checksum: 101011000110111100101111001110
top:      10101
bottom:        1000110111100101111001110
padded:        100011011110010111100111000000
5-bit group:                            10010
xor:           100011011110010111100111010010
generator 0:   111011011010100101011110110010 xor
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011 xor
checksum:      101100101001100101010100101001

checksum: 101100101001100101010100101001
top:      10110
bottom:        0101001100101010100101001
padded:        010100110010101010010100100000
5-bit group:                            00110
xor:           010100110010101010010100100110
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011 xor
checksum:      000110001011110101000000000010

checksum: 000110001011110101000000000010
top:      00011
bottom:        0001011110101000000000010
padded:        000101111010100000000001000000
5-bit group:                            01011
xor:           000101111010100000000001001011
generator 0:   111011011010100101011110110010 xor
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      011000110100001101100110010100

checksum: 011000110100001101100110010100
top:      01100
bottom:        0110100001101100110010100
padded:        011010000110110011001010000000
5-bit group:                            01101
xor:           011010000110110011001010001101
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101 xor
generator 4:   101010000101000110001010110011
checksum:      111001111110000001100010101010

checksum: 111001111110000001100010101010
top:      11100
bottom:        1111110000001100010101010
padded:        111111000000110001010101000000
5-bit group:                            01000
xor:           111111000000110001010101001000
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101 xor
generator 4:   101010000101000110001010110011 xor
checksum:      110110111101000101110111011100

checksum: 110110111101000101110111011100
top:      11011
bottom:        0111101000101110111011100
padded:        011110100010111011101110000000
5-bit group:                            10101
xor:           011110100010111011101110010101
generator 0:   111011011010100101011110110010 xor
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101 xor
generator 4:   101010000101000110001010110011 xor
checksum:      010100111001110011001100100100

checksum: 010100111001110011001100100100
top:      01010
bottom:        0111001110011001100100100
padded:        011100111001100110010010000000
5-bit group:                            00100
xor:           011100111001100110010010000100
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101 xor
generator 4:   101010000101000110001010110011
checksum:      000111111101001101100100110100

checksum: 000111111101001101100100110100
top:      00011
bottom:        1111101001101100100110100
padded:        111110100110110010011010000000
5-bit group:                            10100
xor:           111110100110110010011010010100
generator 0:   111011011010100101011110110010 xor
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      100011101000011111111101001011

checksum: 100011101000011111111101001011
top:      10001
bottom:        1101000011111111101001011
padded:        110100001111111110100101100000
5-bit group:                            00011
xor:           110100001111111110100101100011
generator 0:   111011011010100101011110110010 xor
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011 xor
checksum:      100101010000011101110001100010

checksum: 100101010000011101110001100010
top:      10010
bottom:        1010000011101110001100010
padded:        101000001110111000110001000000
5-bit group:                            10001
xor:           101000001110111000110001010001
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011 xor
checksum:      100100011111110110000010001111

checksum: 100100011111110110000010001111
top:      10010
bottom:        0011111110110000010001111
padded:        001111111011000001000111100000
5-bit group:                            00010
xor:           001111111011000001000111100010
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011 xor
checksum:      000011101010001111110100111100

checksum: 000011101010001111110100111100
top:      00001
bottom:        1101010001111110100111100
padded:        110101000111111010011110000000
5-bit group:                            11101
xor:           110101000111111010011110011101
generator 0:   111011011010100101011110110010 xor
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      001110011101011111000000101111

checksum: 001110011101011111000000101111
top:      00111
bottom:        0011101011111000000101111
padded:        001110101111100000010111100000
5-bit group:                            00011
xor:           001110101111100000010111100011
generator 0:   111011011010100101011110110010 xor
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      001101001001011100010111000110

checksum: 001101001001011100010111000110
top:      00110
bottom:        1001001011100010111000110
padded:        100100101110001011100011000000
5-bit group:                            01100
xor:           100100101110001011100011001100
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      011100010010010010111101011011

checksum: 011100010010010010111101011011
top:      01110
bottom:        0010010010010111101011011
padded:        001001001001011110101101100000
5-bit group:                            11101
xor:           001001001001011110101101111101
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101 xor
generator 4:   101010000101000110001010110011
checksum:      001100100101100100111100110111

checksum: 001100100101100100111100110111
top:      00110
bottom:        0100101100100111100110111
padded:        010010110010011110011011100000
5-bit group:                            00011
xor:           010010110010011110011011100011
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      101010001110000111000101110100

checksum: 101010001110000111000101110100
top:      10101
bottom:        0001110000111000101110100
padded:        000111000011100010111010000000
5-bit group:                            00100
xor:           000111000011100010111010000100
generator 0:   111011011010100101011110110010 xor
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011 xor
checksum:      001000110100010000001001111111

checksum: 001000110100010000001001111111
top:      00100
bottom:        0110100010000001001111111
padded:        011010001000000100111111100000
5-bit group:                            01111
xor:           011010001000000100111111101111
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      000100100000010101011000010101

checksum: 000100100000010101011000010101
top:      00010
bottom:        0100000010101011000010101
padded:        010000001010101100001010100000
5-bit group:                            11000
xor:           010000001010101100001010111000
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      110110011110100100110011010101

checksum: 110110011110100100110011010101
top:      11011
bottom:        0011110100100110011010101
padded:        001111010010011001101010100000
5-bit group:                            10100
xor:           001111010010011001101010110100
generator 0:   111011011010100101011110110010 xor
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101 xor
generator 4:   101010000101000110001010110011 xor
checksum:      000101001001010001001000000101

checksum: 000101001001010001001000000101
top:      00010
bottom:        1001001010001001000000101
padded:        100100101000100100000010100000
5-bit group:                            00110
xor:           100100101000100100000010100110
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      000010111100101100111011001011

checksum: 000010111100101100111011001011
top:      00001
bottom:        0111100101100111011001011
padded:        011110010110011101100101100000
5-bit group:                            01110
xor:           011110010110011101100101101110
generator 0:   111011011010100101011110110010 xor
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      100101001100111000111011011100

checksum: 100101001100111000111011011100
top:      10010
bottom:        1001100111000111011011100
padded:        100110011100011101101110000000
5-bit group:                            11110
xor:           100110011100011101101110011110
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011 xor
checksum:      101010001101010011011101000000

checksum: 101010001101010011011101000000
top:      10101
bottom:        0001101010011011101000000
padded:        000110101001101110100000000000
5-bit group:                            10110
xor:           000110101001101110100000010110
generator 0:   111011011010100101011110110010 xor
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011 xor
checksum:      001001011110011100010011101101

checksum: 001001011110011100010011101101
top:      00100
bottom:        1011110011100010011101101
padded:        101111001110001001110110100000
5-bit group:                            00000
xor:           101111001110001001110110100000
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      110001100110011000010001011010

checksum: 110001100110011000010001011010
top:      11000
bottom:        1100110011000010001011010
padded:        110011001100001000101101000000
5-bit group:                            00000
xor:           110011001100001000101101000000
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101 xor
generator 4:   101010000101000110001010110011 xor
checksum:      100100011001101101101000101110

checksum: 100100011001101101101000101110
top:      10010
bottom:        0011001101101101000101110
padded:        001100110110110100010111000000
5-bit group:                            00000
xor:           001100110110110100010111000000
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101 xor
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011 xor
checksum:      000000100111111010100100011110

checksum: 000000100111111010100100011110
top:      00000
bottom:        0100111111010100100011110
padded:        010011111101010010001111000000
5-bit group:                            00000
xor:           010011111101010010001111000000
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101
generator 4:   101010000101000110001010110011
checksum:      010011111101010010001111000000

checksum: 010011111101010010001111000000
top:      01001
bottom:        1111101010010001111000000
padded:        111110101001000111100000000000
5-bit group:                            00000
xor:           111110101001000111100000000000
generator 0:   111011011010100101011110110010 xor
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010
generator 3:   111101010000100011001111011101 xor
generator 4:   101010000101000110001010110011
checksum:      111000100011000001110001101111

checksum: 111000100011000001110001101111
top:      11100
bottom:        0100011000001110001101111
padded:        010001100000111000110111100000
5-bit group:                            00000
xor:           010001100000111000110111100000
generator 0:   111011011010100101011110110010
generator 1:   100110010100001000111001101101
generator 2:   011110101000010001100111111010 xor
generator 3:   111101010000100011001111011101 xor
generator 4:   101010000101000110001010110011 xor
checksum:      011000011101001100010101110100

For our example, this gives us a resulting checksum value of:

checksum = 011000011101001100010101110100

5. Constant

Lastly, we XOR the current checksum value with a constant.

The constant we use depends on the version of the ScriptPubKey (see Bech32m):

Version 0  = 000000000000000000000000000001
Version 1+ = 101011110010000011000010100011

Our example is a P2WPKH ScriptPubKey, which is version 0:

checksum = 011000011101001100010101110100
constant = 000000000000000000000000000001
result   = 011000011101001100010101110101

6. Split into 5-bit groups

Finally, we can split our 30-bit checksum into 6 groups of 5-bits:

checksum = 011000011101001100010101110101
checksum = 01100 00111 01001 10001 01011 10101

This is our final checksum.

Code

See encode or decode for the checksum algorithm.

Bech32m

BIP 350

Bech32m refers to a minor adjustment made to the checksum algorithm for version 1 Bech32 addresses onwards.

The only difference is that you use a different constant before calculating the final checksum value:

Version Constant Address Type(s)
0 0b000000000000000000000000000001 P2WPKH, P2WSH
1+ 0b101011110010000011000010100011 P2TR

Everything else about the Bech32 encoding remains the same.

This change fixes a problem where if the final character of the address is "p", inserting or removing any number of "q" characters does not make the checksum invalid.

This isn't a major issue, as existing P2WPKH and P2WSH addresses are not affected due to the fact that they're restricted to two specific lengths. Nonetheless, moving forward this change ensures that the checksum will be reliable for all future addresses.

It's easier to think of this as the new default encoding method for "Bech32". In other words, version 0 locking scripts (P2WPKH and P2WSH) use a different "legacy" constant.

Benefits

What are the advantages of Bech32?

Bech32 is more user-friendly and more efficient than the legacy Base58 format for addresses.

In short, it's an upgrade compared to Base58.

User-friendly

Bech32 addresses are more user-friendly than Base32 addresses for three reasons:

1. Case-insensitive

Bech32 addresses do not use a combination of uppercase and lowercase letters, which makes them easier to type out and read out loud compared to Base58.

So if you're giving someone your address over the phone, you no longer need to constantly switch between saying "uppercase x, lowercase y...", and so on.

Bech32 addresses are typically all lowercase, but it's perfectly fine to use all uppercase (which is how they'll get stored in a QR code).

To prevent confusion, Bech32 addresses should not use a combination of uppercase and lowercase letters. A wallet should consider a mixed-case Bech32 address as invalid.

The fact that Bech32 uses fewer characters compared to Base58 (i.e. base 32 instead of base 58) means that addresses are typically longer, but having all the characters in a single case makes Bech32 addresses easier to use overall.

2. Friendly character set

This is not really an "upgrade" as Base58 does something similar, but Bech32 does not use characters that look similar to each other.

To be precise, the data part of the address uses all alphanumeric characters except for "1", "b", "i", and "o":

Bitcoin Base32 Character Set

0 1 2 3 4 5 6 7 8 9
a b c d e f g h i j k l m n o p q r s t u v w x y z

So out of the 36 possible alphanumeric characters, 4 of the least distinctive ones have been removed to leave 32 characters in total.

This is slightly different to pre-existing "base 32" character sets. For example:

The human-readable part is not restricted to using the base 32 characters above. It can contain any US-ASCII character (in the range 33-126), so that's why you can use a "b" at the start of an address.

3. Better checksum

Bech32 addresses use an improved checksum algorithm that allows you to detect and fix errors in the address.

To summarize the differences:

So in short, the Bech32 checksum is smarter.

Efficient

Bech32 addresses are more efficient than Base32 addresses for three reasons:

1. Smaller QR codes

The fact that Bech32 addresses are single-case allows you to encode them into QR codes using alphanumeric mode.

This means you can create more compact QR codes, because Base58 requires both uppercase and lowercase letters (which means you cannot use alphanumeric mode) whereas Bech32 does not.

For example:

Base58 Address

1MHKKX3cN2RnWrxnzg9kLfPzi6vCd1B2H7

Example Base58 address QR code (case sensitive).

Bech32 Address

BC1QMEU8D90HWHFHM49GHGN5ZFGEXDPJSSPZGN28T4

Example Bech32 address QR code (case-insensitive).

As you can see, even though the Bech32 address has more characters, the ability to use alphanumeric mode means the QR code uses less data overall.

The alphanumeric mode for QR codes only support uppercase letters. So that's why when you scan a QR code containing a Bech32 address it will typically show up in all uppercase. This is perfectly fine, as Bech32 addresses are case-insensitive.

2. Faster encoding

It's faster to calculate a Bech32 checksum than a Base58 checksum, which means it's faster to encode Bech32 addresses.

I know the Bech32 checksum algorithm looks pretty complicated, but it's still faster than the double-SHA256 required to create the Base58 checksum.

3. Faster decoding

The characters in a Bech32 address map to specific values, which is faster than the modular arithmetic on big numbers required to decode a Base58 address.

Base58 is not spectacularly slow to encode/decode compared to Bech32, but Bech32 is more efficient nonetheless.

Etymology

Where does the name "Bech32" come from?

The name "Bech32" (besh thirty-two) comes from the fact that the address uses base32 characters, and the checksum uses BCH codes for the error detection/correction algorithm.

So if you smush "base32" and "BCH" together, you get "Bech32". Kind of.

"Bech" contains the characters BCH (the error detection algorithm used) and sounds a bit like "base".
Pieter Wuille, BIP 173

It's not perfect, I know. But it'll do.

Summary

Bech32 is simply a better format for addresses compared to Base58.

Base58 was/is handy because it gives you a nice character set to work with, and a simple checksum to detect errors. But Bech32 offers a bunch of useful improvements:

Base58 was a pretty good effort, and you can't blame Satoshi for it not being perfect, as they probably didn't have months to spend constructing the ultimate address format; it was simple and effective. But since then we've had the luxury of time to construct something better.

We still use Base58 for legacy locking scripts, private keys, and extended keys:

But Bech32 is now used for all modern locking scripts:

The only crushing downside of Bech32 is that the base32 character set does not include the letter "b", so I can't construct a vanity address with the word "beer" in it (hence why I still use a Base58 address for donations). But that's just something I need to live with.

Resources