Difficulty
What is the difficulty in Bitcoin?
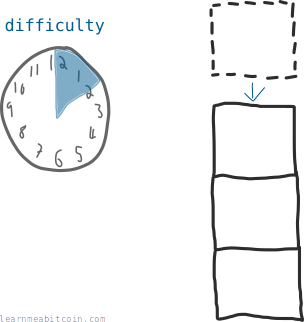
The difficulty is a number that represents how difficult it is for miners to add new blocks of transactions to the blockchain.
It adjusts every 2 weeks to ensure that it takes 10 minutes (on average) to add new blocks to the blockchain.
Why is the difficulty important?
The difficulty ensures that blocks of transactions are added to the blockchain at regular intervals during mining, even as more miners join the network.
If the difficulty stayed the same, it would gradually take less and less time to add new blocks to the blockchain as new miners join the network.
So the difficulty adjustments mean that the blockchain gets updated consistently.
When does the difficulty change?
The difficulty adjusts every 2,016 blocks (roughly every 2 weeks)
At this interval, each node takes the expected time for the last 2,016 blocks to be mined (2016 x 10 minutes), and divides it by the actual time it took:
expected / actual
20160 / actual
If miners were able to solve each block more quickly than expected; say 9 minutes per block for example, you'd get a number like this
20160 / 18144 = 1.11
Each node then uses this number to adjust the difficulty for the next 2,016 blocks:
difficulty x 1.11 = new difficulty
- If the number is greater than 1 (blocks were mined quicker than expected), the difficulty increases.
- If the number is less than 1 (blocks were mined
slower than expected) the difficulty decreases.
And that's it. Every miner on the bitcoin network now works with this new difficulty for the next 2,016 blocks.
The difficulty will only adjust by a factor of 4 at most (i.e. a multiplier not greater than 4, or less than 0.25). This is to prevent abrupt changes from one difficulty period to the next.
How does the difficulty control time between blocks?
Okay, I'll start with a simple example, and build on it from there.
1. Simple example
Let's say I give you a range of numbers from 1 to 100.

Now, let's say you are able to randomly generate a number between 1 and 100 once every minute, and your goal is to generate a number below my target number.
So let's say I set the target at 50:
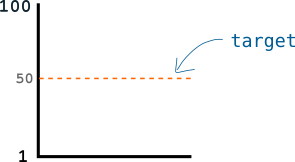
Seeing as you're only able to generate a number once a minute, this should take you 2 minutes on average to find a number below this target value.
But that's too easy. So let's say I lower the target to 20, which means you're only going to be able to generate a winning number 1/5 of the time, or once every 5 minutes:
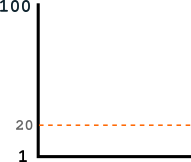
The lower the target, the more difficult it gets to generate a winning number.
So as you can see, I can use the height of the target to control how long it takes you to find a winning number (depending on how many numbers you are able to generate per minute, of course).
It's not going to be exactly 5 minutes every time, because you could get lucky on your first attempt. However, over the long run it will work out to be 5-minute intervals on average.
So what is the difficulty?
Instead of telling you the target value directly, I could give you the target by dividing the range of numbers with a new number:
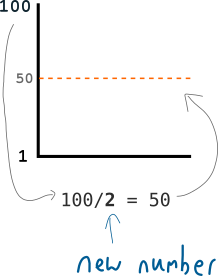
This new number is the difficulty, and it's used to modify the height of the target.
Here's the equation for setting the target using the difficulty:
target = max target / difficulty
So now I can use this difficulty value to help me set the target to any level I want:
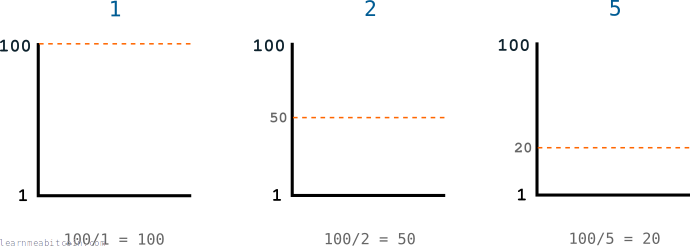
Therefore, I use the difficulty to control the target, which in turn controls how long it takes for you to generate a winning number below the target.
- The difficulty is basically another way of representing the current target.
- The higher the difficulty, the lower the target.
2. Bitcoin example
The difficulty in bitcoin works in exactly the same way – it's used to set a target value, and miners keep generating numbers (hashing their candidate blocks) in the hope that they will find a block hash below the target value:
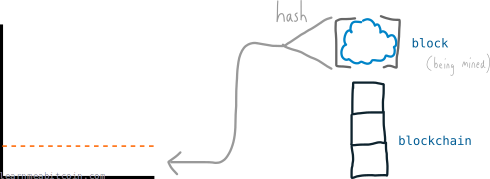
And seeing as miners are able to generate thousands of numbers (hashes) per second, bitcoin uses extremely large numbers for the target:
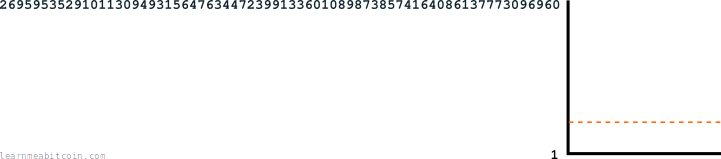
And due to the fact that there are now thousands of miners trying to find winning numbers, to ensure that a winning number is found every 10 minutes (instead of every few seconds), the range of successful numbers ends up being absolutely tiny:

Even though that difficulty number looks big, the target is still absurdly difficult to get under. It's like a lottery.
Hexadecimal numbers
Because these target numbers are so big, we typically display them in the shorter hexadecimal format.

That's why block hashes look like this: 000000000003ba27aa200b1cecaad478d2b00432346c3f1f3986da1afd33e506
But even though it contains letters, it's still a number. So the target is a hexadecimal value, and miners are trying to get a hexadecimal block hash below the target.
In fact, you can easily convert between hexadecimal and "normal" numbers (aka decimal numbers):
| Hexadecimal | 000000000004864c000000000000000000000000000000000000000000000000 |
|---|---|
| Decimal | 1861311314983800126815643622927230076368334845814253369901973504 |
| Hexadecimal | 000000000003ba27aa200b1cecaad478d2b00432346c3f1f3986da1afd33e506 |
|---|---|
| Decimal | 1533267872647776902154320487930659211795065581998445848740226310 |
So that's why you usually see the hash and the target as bunches of numbers and letters – they're in hexadecimal as opposed to decimal (which is what humans are more familiar with).
Just remember that both these decimal and hexadecimal numbers have the same value, and you can easily convert between the two.
Awkwardly, the difficulty is usually given in decimal format, whereas block hashes and targets in hexadecimal:
But as I say, they're both numbers, so you can still work with them if you convert them to the same format.
How do you calculate the difficulty?
The difficulty is calculated by dividing the maximum possible target value by the target for the current block.
The max target is the target that was set for the very first block:
max target = 0x00000000ffff0000000000000000000000000000000000000000000000000000
So to work out the difficulty for block 100,000 for example, we just need to find out what the target for that block was:
target = 0x000000000004864c000000000000000000000000000000000000000000000000
Now, if we convert both of these values to decimal and divide them, we get the difficulty:
difficulty = max target / target
difficulty = 0x00000000ffff0000000000000000000000000000000000000000000000000000 / 0x000000000004864c000000000000000000000000000000000000000000000000
difficulty = 26959535291011309493156476344723991336010898738574164086137773096960 / 1861311314983800126815643622927230076368334845814253369901973504
difficulty = 14484.162361
So as you can see, the difficulty is just a representation of how far the current target has moved from the maximum possible target value.
Internally in Bitcoin, it's only the target that adjusts. So the difficulty is just a way of representing the change.
How do you calculate the target from the difficulty?
The difficulty is calculated from the target. However, you can always work backwards to calculate the target from the difficulty if you want to.
Let's use the difficulty to work out target for block 100,000.
We'll do it using decimal numbers (mostly), because they're easier to understand.
Here's the difficulty:
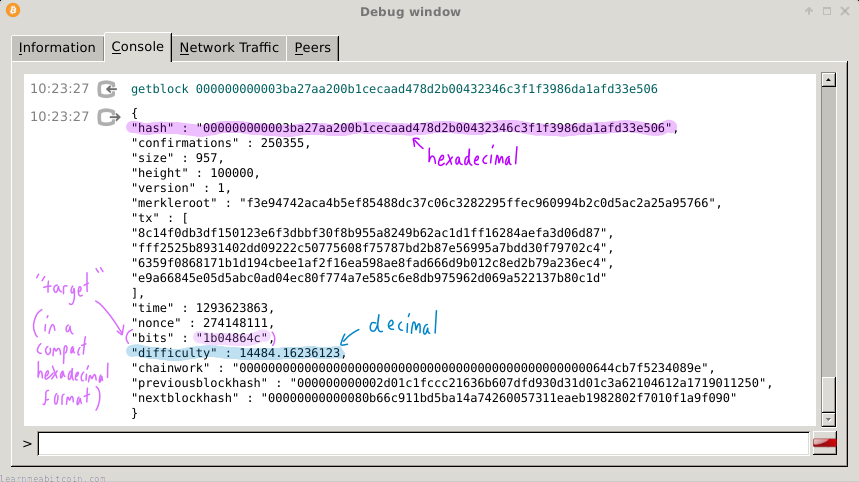
bitcoin-cli getblockheader 000000000003ba27aa200b1cecaad478d2b00432346c3f1f3986da1afd33e506
{
"hash" : "000000000003ba27aa200b1cecaad478d2b00432346c3f1f3986da1afd33e506",
...
"height" : 100000,
...
"difficulty" : 14484.16236123,
...
}
Lovely.
Now, let's note down the equation we're going to use to find the target:
target = max target / difficulty
Let's get the max target and difficulty ready to insert it into the equation.
max target = 0x00000000ffff0000000000000000000000000000000000000000000000000000
difficulty = 14484.162361
- The max target is a fixed value; it's the initial target that was set for the very first block.
- The 0x a prefix is used to signify hexadecimal values (the 0x isn't part of the number). The presence of letters within the value is usually a giveaway (but not always).
- I got the difficulty from the block header information above.
The max target is currently in hexadecimal format though, so let's convert that to decimal.
max target = 26959535291011309493156476344723991336010898738574164086137773096960
Now we can just plug these numbers into the equation and away we go:
target = max target / difficulty
target = 26959535291011309493156476344723991336010898738574164086137773096960 / 14484.162361
target = 1861311315012765306929610463010191006516769515973403833769533170
Ta da.
So when the miner was trying to solve block 100,000, she wanted to get a hash for her candidate block that would be below 1861311315012765306929610463010191006516769515973403833769533170.
Checking the results
Let's compare this target value with the hash she got for the block to check that she was genuinely successful (i.e. her hash for the block was below the target):
target = 1861311315012765306929610463010191006516769515973403833769533170
hash = 0x000000000003ba27aa200b1cecaad478d2b00432346c3f1f3986da1afd33e506
Oh yeah, the hash is in hexadecimal format. Let's convert from hexadecimal to decimal again so that we can compare the two numbers:
target = 1861311315012765306929610463010191006516769515973403833769533170
hash = 1533267872647776902154320487930659211795065581998445848740226310
Yep, that hash is lower than the target, so the block can be added to the blockchain.
Where can I find the current difficulty?
You can find the current difficulty using the bitcoin-cli getdifficulty command:
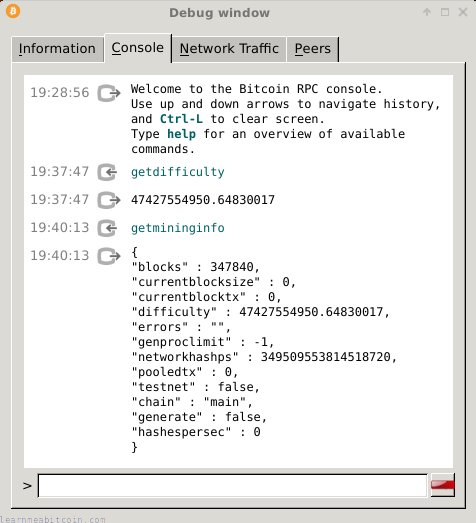
- The current difficulty can also be found within
bitcoin-cli getmininginfo. - Here's a chart showing the change in difficulty over time: blockchain.com/explorer/charts/difficulty
Summary
The target is the actual limbo pole that block hashes have to get below for a new block to be added on the blockchain.
The difficulty is just a measure of how much the target has moved from its initial starting value. Or in other words, how much more difficult it is to mine a block compared to when the blockchain first started.