Little-Endian

tool-6809abbf6ab6b

Little Endian

Convert numbers to big-endian and little-endian byte orders.

+1 Decimal

0d

Hex Bytes (Big Endian)

0x

0 bytes Hex Bytes (Little Endian)

0x

0 bytes

Field Size

Any 2 Bytes 4 Bytes 8 Bytes 12 Bytes 16 Bytes 32 Bytes

0 secs

The term little-endian refers to the order of bytes when storing integers on a computer. It's when the least-significant byte comes first, or more simply, it's when the bytes appear backwards.

Almost all integers in raw bitcoin data are in little-endian byte order, so it's worth getting used to.

Example

What is little-endian?

Let's say we're setting the amount of a transaction output to 12345678 satoshis.

Now, the amount field is 8 bytes in size. So if we convert this value to hexadecimal bytes, it looks like this:

00 00 00 00 00 bc 61 4e

This order of bytes is called big-endian.

We obviously haven't maxed-out this field, as the largest integer this 8-byte field can hold is 0xffffffffffffffff (or 18446744073709551615). This is obvious because there are so many zeros on the left, and as humans we expect to see the biggest numbers on the left.

However, computers (and bitcoin) like to read these bytes from the other direction:

4e 61 bc 00 00 00 00 00

This byte order is called little-endian.

We have the exact same bytes, but they are in reverse order. So instead of reading the smallest bytes from right-to-left, we're now reading them from left-to-right.

Byte Orders

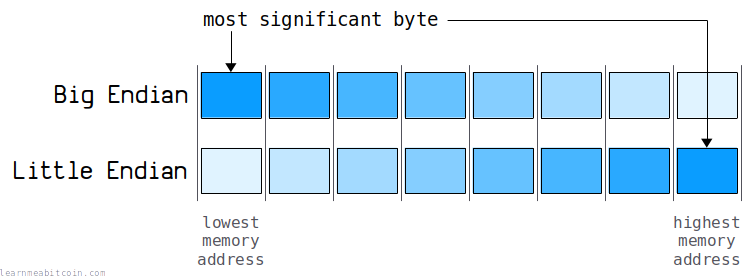
As mentioned, there are two different ways of ordering bytes when storing integers on a computer:

1. Big Endian
2. Little Endian

Some computers use big-endian architecture, and others use little-endian architecture.

1. Big Endian

(Rarely used in Bitcoin)

This is the more "human-readable" format. The byte containing the biggest number comes first:

00 00 00 00 00 bc 61 4e

Or more technically speaking, it's when the most-significant byte is stored at the lowest memory address in a block of bytes. For example:

┌────────────────┬──────────┐
│ Memory Address │ Contents │
├────────────────┼──────────┤
│ 100            │ 0x00     │
│ 101            │ 0x00     │
│ 102            │ 0x00     │
│ 103            │ 0x00     │
│ 104            │ 0x00     │
│ 105            │ 0xbc     │
│ 106            │ 0x61     │
│ 107            │ 0x4e     │
└────────────────┴──────────┘

Memory Address. An address is a location in computer memory. Each byte of memory has its own address. The 100 to 107 addresses are just examples. This is a good 10-minute video on memory addresses.

2. Little Endian

(Commonly used in Bitcoin)

This is the more "computer-readable" format. The byte containing the smallest number comes first:

4e 61 bc 00 00 00 00 00

Or more technically speaking, it's when the most-significant byte is stored at the highest memory address in a block of bytes. For example:

┌────────────────┬──────────┐
│ Memory Address │ Contents │
├────────────────┼──────────┤
│ 100            │ 0x4e     │
│ 101            │ 0x61     │
│ 102            │ 0xbc     │
│ 103            │ 0x00     │
│ 104            │ 0x00     │
│ 105            │ 0x00     │
│ 106            │ 0x00     │
│ 107            │ 0x00     │
└────────────────┴──────────┘

As you can guess, Satoshi was working on a little-endian computer when programming bitcoin.

Terminology

Why is it called "little-endian" and "big-endian"?

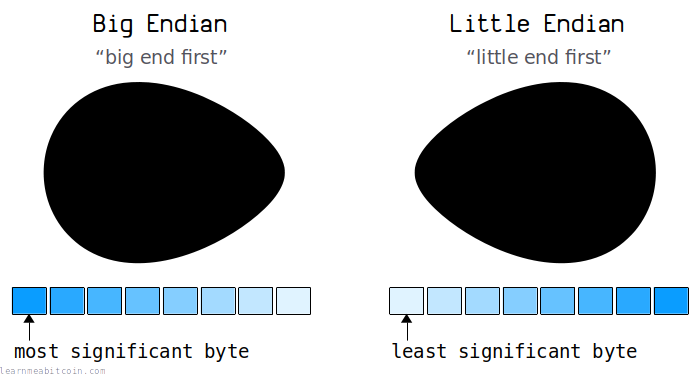
Because of eggs, basically.

The terms "little-endian" and "big-endian" originate from the book Gulliver's Travels (1726). There's a section referring to two different groups of people: one that breaks open eggs from the "little end", and another that breaks open their eggs from the "big end".

These "little end" and "big end" terms were then adopted to describe the two different ways of ordering bytes on a computer.

Usage

When do we use little-endian in bitcoin?

You'll find little-endian fields in bitcoin any time you're working with integers inside network messages.

The most common places you'll see little-endian is in raw transaction data and raw block headers.

Transaction Data

02000000 <- version (little-endian)
    01 <- input count
        79fe743502ff8cd181121572fececac3feee5ef3034edfb3ccd2bfaa24537dae <- txid
        01000000 <- vout (little-endian)
        6a 473044022...915 <- scriptsig
        fdffffff <- sequence (little-endian)
    01 <- output count
        2a5f020000000000 <- output amount (little-endian)
        19 76a914a9970b7ed051822ea52a088b9c628eb158dd57e588ac <- scriptpubkey
ff30a00 <- locktime (little-endian)

For example, the vout is a 4-byte little-endian field, and in this transaction it is referring to a previous output number of 1. If this field was big-endian, it would be 00000001, but because it's little-endian the bytes are in reverse order 01000000.

Block Header

Here's a raw block header.

00000020 <- version (little-endian)
b91fd2b09d4a8238ad4c814e4fa0ab9ed34bf0f75a3a00000000000000000000 <- previous block hash
330b32016c8176153071283d3e5fe87c2318b3fd41d6ca1b1a8bf12670908e38 <- merkle root
daf0d861 <- time (little-endian)
ab980b17 <- bits (little-endian)
0e69d05c <- nonce (little-endian)

As you can see, all of the little-endian fields are the ones that contain some kind of number.

For example, the time in the block header is a 4-byte little-endian field containing a Unix timestamp. Here it's daf0d861, which in big-endian would be 61d8f0da. If we convert this to decimal we get 1641607386, which is a Unix timestamp for 08 Jan 2022, 02:03:06 UTC.

Converting

How to convert between big-endian and little-endian

If you're working with strings, a quick and dirty way to reverse the byte order is to split up the string into an array of 2-character chunks (2 hex characters = 1 byte), and then reverse the array.

# integer
amount = 12345678

# ----------
# Hex Strings
# -----------

# convert integer to 8-byte hexadecimal string (big endian)
big_endian = amount.to_s(16).rjust(16, "0") # 16 hex characters = 8 bytes
puts big_endian #=> 0000000000bc614e

# convert big-endian hexadecimal string to little-endian (reverse the byte order)
little_endian = big_endian.scan(/../).reverse.join
puts little_endian #=> 4e61bc0000000000

Alternatively (and more professionally), you can use the pack and unpack functions to convert between numbers and actual raw bytes.

# integer
amount = 12345678

# -----
# Bytes - pack() and unpack()
# -----
# Pack directives for integers:
#
# C< = 8-bit  integer (unsigned), (a single byte has no endianness)
# S< = 16-bit integer (unsigned), little-endian
# L< = 32-bit integer (unsigned), little-endian
# Q< = 64-bit integer (unsigned), little-endian
#
# v  = 16-bit integer (unsigned), little-endian (same as <S)
# V  = 32-bit integer (unsigned), little-endian (same as <L)
#
# Note: The "<" forces little-endian. Without it pack() will use the endianness of your system (i.e. native byte order).
# Note: An asterisk "*" will repeat the directive for all remaining elements.
# Source: https://ruby-doc.org/core-3.1.0/Array.html#method-i-pack

# convert integer to 8 bytes in little-endian
bytes = [amount].pack("Q<")

# convert bytes to hexadecimal string
string = bytes.unpack("H*")[0]
puts string #=> 4e61bc0000000000

And here's a quick and dirty way to convert between big-endian and little-endian on the command line:

echo -n acbd | tac -rs ..

Thanks to Greg Tonoski for this handy bash one-liner.

Popularity

Is little-endian a popular choice with bitcoin developers?

Not entirely. There have been discussions about it since 2011:

So if you think working with little-endian is awkward, you're not alone.

There are basically two camps:

1. Little-endian makes sense because most modern computers use a little-endian architecture.
2. Big-endian makes sense because most communications over the network use big-endian.

Personally I think it would be much easier to use big-endian everywhere.

It would make developing on bitcoin much more straightforward, as it would remove the need to look up documentation all the time to find out "is this field little-endian?". Plus, transaction IDs and block hashes have their byte orders reversed to appear in a big-endian format when displayed, so using big-endian would make everything consistent. Not to mention the fact that big-endian is more human-readable.

But none of this matters. Bitcoin has been little-endian since the beginning, and changing it would result in a controversial hard fork with minimal benefit, so it's not going to change.

On the plus side, it does give you the opportunity to learn the difference between little-endian and big-endian byte orders. I didn't even know byte order was a thing until I started playing with bitcoin data.

Why does bitcoin use little-endian?

Because Satoshi developed Bitcoin on a computer with little-endian architecture.

It might seem unusual at first, but the little-endian byte order is actually more common than you think:

So whilst it looks backwards to humans, it's pretty standard for computers.

import sys
print("System Byte Order:", sys.byteorder)

You wouldn't usually care about the underlying architecture of your system in day-to-day programming. But endianness may become relevant when you start working with the raw bytes of data that get sent across a network (e.g. transaction data).

Summary

Little-endian is the byte order we use for storing integers (and other multi-byte structures such as the bits field) in raw bitcoin data such as transactions and block headers.

To the human eye, little-endian looks like the bytes are in reverse order. However, many modern computers use little-endian architecture, and Satoshi programmed the first version of Bitcoin on a little-endian computer, so that's why we use little-endian in Bitcoin.

It would probably be easier from a development perspective to have everything in big-endian, but little-endian is what Satoshi went with, so you just have to get used to it.

Welcome to bitcoin programming.

Resources

• Big and Little Endian - cs.umd.edu