0100000002f60b5e96f09422354ab150b0e506c4bffedaf20216d30059cc5a3061b4c83dff000000004a493046022100e26d9ff76a07d68369e5782be3f8532d25ecc8add58ee256da6c550b52e8006b022100b4431f5a9a4dcb51cbdcaae935218c0ae4cfc8aa903fe4e5bac4c208290b7d5d01fffffffff7272ef43189f5553c2baea50f59cde99b3220fd518884d932016d055895b62d000000004a493046022100a2ab7cdc5b67aca032899ea1b262f6e8181060f5a34ee667a82dac9c7b7db4c3022100911bc945c4b435df8227466433e56899fbb65833e4853683ecaa12ee840d16bf01ffffffff0100e40b54020000001976a91412ab8dc588ca9d5787dde7eb29569da63c3a238c88ac00000000Public Key Hash
A shortened public key
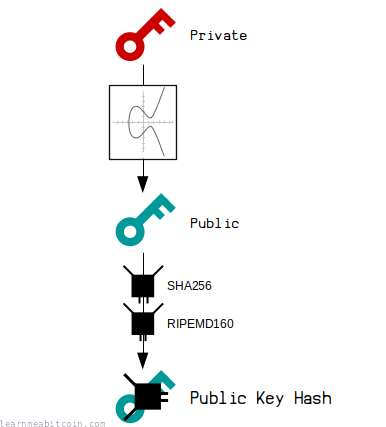
A public key hash is the hash of a public key. So no surprises there.
Hashing produces a shortened version of the public key, which ultimately means you can create a shorter address that is easier to share with other people.
This public key hash gets used within the P2PKH (Pay To Public Key Hash) and P2WPKH (Pay To Witness Public Key Hash) locking scripts, which are the most common locking scripts used when sending bitcoins to an address via a bitcoin wallet.
Creating
How do you create a public key hash?
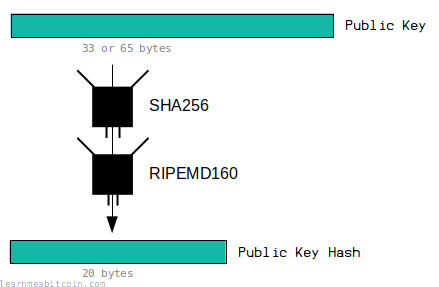
A public key hash is the HASH160 of a public key.
For example, if this is your public key:
02e3af28965693b9ce1228f9d468149b831d6a0540b25e8a9900f71372c11fb277
This is the public key hash:
1e51fcdc14be9a148bb0aaec9197eb47c83776fb
Code

 copied
copied copied
copied# HASH160 Function
def hash160(data)
# Convert data to binary before hashing
binary = [data].pack("H*")
# SHA-256 first
sha256 = Digest::SHA256.digest(binary)
# RIPEMD-160 second
ripemd160 = Digest::RMD160.digest(sha256)
# Convert back to hexadecimal from binary
hash160 = ripemd160.unpack("H*").join
return hash160
end
# Public Key
publickey = "02e3af28965693b9ce1228f9d468149b831d6a0540b25e8a9900f71372c11fb277"
# Public Key Hash
puts hash160(publickey) #=> 1e51fcdc14be9a148bb0aaec9197eb47c83776fb
RIPEMD-160
RIPEMD-160 produces a 20 byte (160 bit) digest.
This is smaller than the original public key (65 bytes uncompressed, 33 bytes compressed).
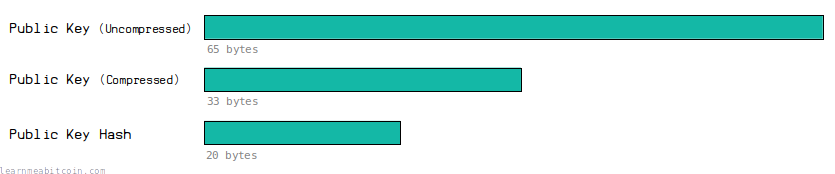
This means that the eventual address we create from it will contain fewer characters than a full public key, making it easier to pass around.
Usage
How are public key hashes used in Bitcoin?
The main reason for hashing a public key is so that it can be shortened before converting it to an address.
So when someone sends bitcoins to our address using a wallet, they're actually locking an output to our public key hash rather than our full public key:
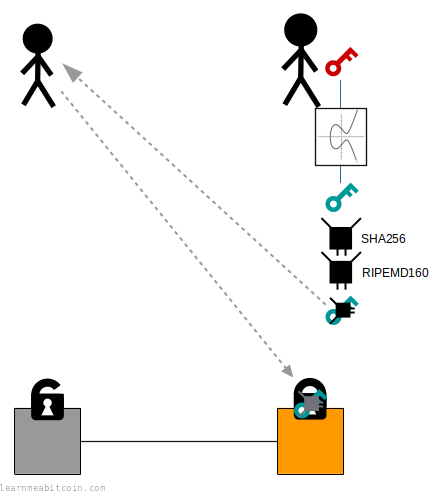
When we come to spend these bitcoins in a future transaction, we then provide the original public key along with a signature inside the unlocking code for the input:
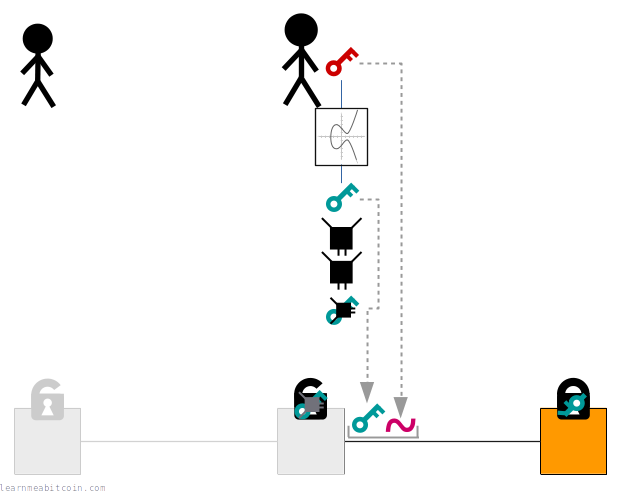
When a node validates this transaction it will:
- Check that the public key hashes to the public key hash inside the lock.
- Verify the signature against the public key as normal.
So basically, using a public key hash adds an extra step when it comes to locking and unlocking bitcoins, but the tradeoff is that we get to use shorter addresses.
Location
Where can you find public key hashes?
A public key hash can be found within transactions that use P2PKH and P2WPKH locking scripts.
Here are some examples of public key hashes within raw transactions in the blockchain.
P2PKH
Pay To Public Key Hash
A public key hash can be found inside the ScriptPubKey of a P2PKH (Pay To Public Key Hash):
{
"version": "01000000",
"inputcount": "02",
"inputs": [
{
"txid": "f60b5e96f09422354ab150b0e506c4bffedaf20216d30059cc5a3061b4c83dff",
"vout": "00000000",
"scriptsigsize": "4a",
"scriptsig": "493046022100e26d9ff76a07d68369e5782be3f8532d25ecc8add58ee256da6c550b52e8006b022100b4431f5a9a4dcb51cbdcaae935218c0ae4cfc8aa903fe4e5bac4c208290b7d5d01",
"sequence": "ffffffff"
},
{
"txid": "f7272ef43189f5553c2baea50f59cde99b3220fd518884d932016d055895b62d",
"vout": "00000000",
"scriptsigsize": "4a",
"scriptsig": "493046022100a2ab7cdc5b67aca032899ea1b262f6e8181060f5a34ee667a82dac9c7b7db4c3022100911bc945c4b435df8227466433e56899fbb65833e4853683ecaa12ee840d16bf01",
"sequence": "ffffffff"
}
],
"outputcount": "01",
"outputs": [
{
"amount": "00e40b5402000000",
"scriptpubkeysize": "19",
"scriptpubkey": "76a91412ab8dc588ca9d5787dde7eb29569da63c3a238c88ac"
}
],
"locktime": "00000000"
}
Transaction: 6f7cf9580f1c2dfb3c4d5d043cdbb128c640e3f20161245aa7372e9666168516
The full public key is then revealed in the ScriptSig when this output is used as an input in a spending transaction:
01000000030dd7891efbf67da47c651531db8aab3144ed7a524e4ae1e30b773525e27ddd7b000000004948304502206f6a68710a51f77e5a1fa4d1037a23a76723724a51fd54710949e0189ee02dfa022100dad3454ade12fe84f3818e14c41ec2e02bbb154dd3136a094cdf86f67ebbe0b601ffffffff16851666962e37a75a246101f2e340c628b1db3c045d4d3cfb2d1c0f58f97c6f000000008b48304502203f004eeed0cef2715643e2f25a27a28f3c578e94c7f0f6a4df104e7d163f7f8f022100b8b248c1cfd8f77a0365107a9511d759b7544d979dd152a955c867afac0ef7860141044d05240cfbd8a2786eda9dadd520c1609b8593ff8641018d57703d02ba687cf2f187f0cee2221c3afb1b5ff7888caced2423916b61444666ca1216f26181398cffffffffffda5d38e91fd9a0d92872d51f83cb746fc7bf5d3ff13402f8d0d5ed60ddc79c0000000049483045022100b6fd43f2fa16e092678283f64d2e08fb2070b4af2b3ddfb9ca3c5e238288acaa02200c5a28e0a4fc1a540f6eeb30ccc4788050eae46964fe33ccb4500c3de1320c2501ffffffff02c0c62d00000000001976a91417194e1bd175fb5b1b2a1f9d221f6f5c29e1928388ac00c817a8040000001976a91465bda9b05f7e9a8f96a7f4ba0996a877708ef90888ac00000000
{
"version": "01000000",
"inputcount": "03",
"inputs": [
{
"txid": "0dd7891efbf67da47c651531db8aab3144ed7a524e4ae1e30b773525e27ddd7b",
"vout": "00000000",
"scriptsigsize": "49",
"scriptsig": "48304502206f6a68710a51f77e5a1fa4d1037a23a76723724a51fd54710949e0189ee02dfa022100dad3454ade12fe84f3818e14c41ec2e02bbb154dd3136a094cdf86f67ebbe0b601",
"sequence": "ffffffff"
},
{
"txid": "16851666962e37a75a246101f2e340c628b1db3c045d4d3cfb2d1c0f58f97c6f",
"vout": "00000000",
"scriptsigsize": "8b",
"scriptsig": "48304502203f004eeed0cef2715643e2f25a27a28f3c578e94c7f0f6a4df104e7d163f7f8f022100b8b248c1cfd8f77a0365107a9511d759b7544d979dd152a955c867afac0ef7860141044d05240cfbd8a2786eda9dadd520c1609b8593ff8641018d57703d02ba687cf2f187f0cee2221c3afb1b5ff7888caced2423916b61444666ca1216f26181398c",
"sequence": "ffffffff"
},
{
"txid": "ffda5d38e91fd9a0d92872d51f83cb746fc7bf5d3ff13402f8d0d5ed60ddc79c",
"vout": "00000000",
"scriptsigsize": "49",
"scriptsig": "483045022100b6fd43f2fa16e092678283f64d2e08fb2070b4af2b3ddfb9ca3c5e238288acaa02200c5a28e0a4fc1a540f6eeb30ccc4788050eae46964fe33ccb4500c3de1320c2501",
"sequence": "ffffffff"
}
],
"outputcount": "02",
"outputs": [
{
"amount": "c0c62d0000000000",
"scriptpubkeysize": "19",
"scriptpubkey": "76a91417194e1bd175fb5b1b2a1f9d221f6f5c29e1928388ac"
},
{
"amount": "00c817a804000000",
"scriptpubkeysize": "19",
"scriptpubkey": "76a91465bda9b05f7e9a8f96a7f4ba0996a877708ef90888ac"
}
],
"locktime": "00000000"
}
Transaction: 12e753ef5cc30925a6eee2c457aa7f53022443ca013ea81882a6b59b69e342a6
P2WPKH
Pay To Witness Public Key Hash
A public key hash can be found inside the ScriptPubKey of a P2WPKH (Pay To Witness Public Key Hash):
020000000001016972546966be990440a0665b73d0f4c3c942592d1f64d1033717aaa3e2c2ec913300000000ffffffff024087100000000000160014841b80d2cc75f5345c482af96294d04fdd66b2b760e31600000000001600142e8734f8e263e516d47fcaa2dfe1bd01e0dc935802473044022042e5e3ed2a41214ae864634b6fde33ca2ff312f3d89d6aa3e14c026d50d8ed3202206c38dcd0432a0724490356fbf599cdae40e334c3667a9253f8f4cc57cf3c4480012103f465315805ed271eb972e43d84d2a9e19494d10151d9f6adb32b8534bfd764ab00000000
{
"version": "02000000",
"marker": "00",
"flag": "01",
"inputcount": "01",
"inputs": [
{
"txid": "6972546966be990440a0665b73d0f4c3c942592d1f64d1033717aaa3e2c2ec91",
"vout": "33000000",
"scriptsigsize": "00",
"scriptsig": "",
"sequence": "ffffffff"
}
],
"outputcount": "02",
"outputs": [
{
"amount": "4087100000000000",
"scriptpubkeysize": "16",
"scriptpubkey": "0014841b80d2cc75f5345c482af96294d04fdd66b2b7"
},
{
"amount": "60e3160000000000",
"scriptpubkeysize": "16",
"scriptpubkey": "00142e8734f8e263e516d47fcaa2dfe1bd01e0dc9358"
}
],
"witness": [
{
"stackitems": "02",
"0": {
"size": "47",
"item": "3044022042e5e3ed2a41214ae864634b6fde33ca2ff312f3d89d6aa3e14c026d50d8ed3202206c38dcd0432a0724490356fbf599cdae40e334c3667a9253f8f4cc57cf3c448001"
},
"1": {
"size": "21",
"item": "03f465315805ed271eb972e43d84d2a9e19494d10151d9f6adb32b8534bfd764ab"
}
}
],
"locktime": "00000000"
}
Transaction: c178d8dacdfb989f9d4fa45828ed188cd54a0414d625c3e61e75c5e3ac15a83a
Note: This transaction also has a second P2WPKH output containing another public key hash, but I've only highlighted the first one as an example.
The full public key is then revealed in the Witness when this output is used as an input in a spending transaction:
020000000001013aa815ace3c5751ee6c325d614044ad58c18ed2858a44f9d9f98fbcddad878c10000000000ffffffff01344d10000000000016001430cd68883f558464ec7939d9f960956422018f0702483045022100c7fb3bd38bdceb315a28a0793d85f31e4e1d9983122b4a5de741d6ddca5caf8202207b2821abd7a1a2157a9d5e69d2fdba3502b0a96be809c34981f8445555bdafdb012103f465315805ed271eb972e43d84d2a9e19494d10151d9f6adb32b8534bfd764ab00000000
{
"version": "02000000",
"marker": "00",
"flag": "01",
"inputcount": "01",
"inputs": [
{
"txid": "3aa815ace3c5751ee6c325d614044ad58c18ed2858a44f9d9f98fbcddad878c1",
"vout": "00000000",
"scriptsigsize": "00",
"scriptsig": "",
"sequence": "ffffffff"
}
],
"outputcount": "01",
"outputs": [
{
"amount": "344d100000000000",
"scriptpubkeysize": "16",
"scriptpubkey": "001430cd68883f558464ec7939d9f960956422018f07"
}
],
"witness": [
{
"stackitems": "02",
"0": {
"size": "48",
"item": "3045022100c7fb3bd38bdceb315a28a0793d85f31e4e1d9983122b4a5de741d6ddca5caf8202207b2821abd7a1a2157a9d5e69d2fdba3502b0a96be809c34981f8445555bdafdb01"
},
"1": {
"size": "21",
"item": "03f465315805ed271eb972e43d84d2a9e19494d10151d9f6adb32b8534bfd764ab"
}
}
],
"locktime": "00000000"
}
Transaction: 1674761a2b5cb6c7ea39ef58483433e8735e732f5d5815c9ef90523a91ed34a6
History
Why do we use public key hashes in the first place?
Because that's how Satoshi chose to make addresses work in the first release of Bitcoin.
I believe it was most likely because Satoshi was not aware that you could use compressed public keys (33 bytes instead of 65 bytes), so hashing the public key was a way to create a much shorter address that you could share with other people.

So maybe if Satoshi was familiar with the existence of compressed public keys, we would have addresses for the simpler P2PK locking script type instead, and P2PKH would not be required.
To make Bitcoin Addresses short, they are a hash of the public key, not the public key itself.
It's just to get shorter addresses. Regular public keys are 65 bytes long, which is much too long to be convenient. Compressed public keys are 33 bytes and could potentially be used instead of hashes, though these are a little longer than 20-byte hashes. It also seems likely that Satoshi didn't know about compressed public keys or wasn't comfortable with using them when he designed Bitcoin.
Alternative Theory: Extra Security
An alternative theory is that using the hashing the public key provides an extra layer of security.
For example, if we give away our public key directly when we want to receive bitcoins, the "only" thing protecting you from attackers trying to get to your private key is the elliptic curve.
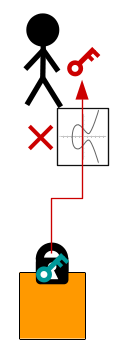
However, if we give out a public key hash instead, attackers would have to crack both the RIPEMD-160 and SHA-256 hash functions, as well as deal with the elliptic curve problem.
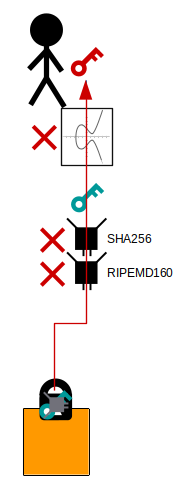
So basically, whilst you have bitcoins sitting in the blockchain, the hash functions act as extra hurdles that attackers must jump over to try and get to our private key (and steal our bitcoins).
So is the elliptic curve not enough protection?
It's actually excellent protection.
Thanks to the properties of elliptic curve multiplication, it's impossibly difficult to work backwards from a public key to a private key. This is known as the "elliptic curve discrete logarithm problem".
However, if by some miracle this problem is solved, there are still two different hash functions to fall back on to protect our private key.
But don't you still give away your public key?
Yes. But in this system your public key is only given away at the last moment (when you come to spend your bitcoins).
The theory is that if someone wants to crack your private key, they will have a small amount of time to do it before your transaction propagates the network and gets mined into a block. Therefore, this is more secure than leaving your raw public key exposed from the start.
However, this theory isn't popular with everyone:
I think this advantage of keeping the pubkey secret is very marginal at best, and more commonly an illusion. Pretty much anything interesting beyond simple payments (multisig, Lightning, ...) involves sharing your public keys with not entirely trusted parties. Bitcoin's security relies on ECDSA being unbreakable even when public keys are revealed; as far as I'm concerned the "pubkeys are only briefly exposed is an advantage" is cargo cult.
Summary
It would certainly be easier if we didn't use public key hashes at all and just used public keys instead.
This would mean that we could just use the simpler P2PK locking script, rather than having to use the extra step involved in P2PKH and P2WPKH where we lock an output to a public key hash first, and then provide the original public key later on.
However, Satoshi had users in mind when developing bitcoin, and they felt that shortening the public key as much as possible before converting to an address would be more user-friendly, so that's why we still continue to use public key hashes throughout Bitcoin today.
So having slightly more complex locking scripts by using public key hashes instead of just public keys is the tradeoff for getting shorter addresses. It's a bit unnecessary in retrospect, but if you've managed to design and code a revolutionary decentralized electronic payment system all by yourself, I guess you can be forgiven for hashing something when you don't really need to.
In conclusion, creating a public key hash is pretty straightforward, and when you understand the reason behind shortening the public key in the first place, the design of P2PKH and P2WPKH make much more sense.